ISSN: 0970-938X (Print) | 0976-1683 (Electronic)
Biomedical Research
An International Journal of Medical Sciences
Research Article - Biomedical Research (2017) Volume 28, Issue 20
A novel method to replace classical spinal manometry: a non-inferiority study
Background: For over 200 years, researchers studied CSF pressure, yet there is limited knowledge on its influence on diseases and syndromes such as Post-Lumbar Puncture Headache (PLPH). In this study, a practical and cost-effective method was proposed to measure CSF pressure.
Methods: In this study, a prototype of a novel device to measure CSF pressure is presented. The device is composed of two parts: a drop sensor and a digital chronometer. The drop sensor is composed of an infrared receiver/transmitter where CSF drops are captured. CSF drop time intervals are calculated by the chronometer. Novel device was tested on a non-pulsatile CSF model filled with Ringer lactate using seven different types of spinal needles. A reference table was constructed from these measurements. The accuracy of the novel method was tested with a blind study. The reference table was used to predict the CSF pressure.
Results: The novel CSF pressure measurement method is non-inferior to the conventional spinal manometry with a slope range of 0.9704-1.011 within 95% confidence interval (p<0.0001).
Conclusion: The novel device can be used to measure CSF pressure as an alternative to the spinal manometer. Advanced models of the novel device can be developed with sophisticated and more detailed features such as spinal needle inner and outer diameters or brand types and reference tables can be uploaded to the software of the device.
Keywords
Cerebrospinal fluid flow rate, Cerebrospinal fluid pressure, Novel device, Spinal manometer
Introduction
Cerebrospinal Fluid (CSF) pressure has been of interest of researchers as early as 1881 and experimental set-ups to measure CSF pressure date back to 1887 [1]. For clinicians, CSF pressure is of concern for different reasons. While neurologists and paediatricians use CSF pressure for diagnostic Lumbar Puncture (LP), anaesthetists use CSF pressure measurement as a means of investigation during spinal anesthesia [2]. It has been reported that one of the reasons of Post-Lumbar Puncture Headache (PLPH) is increased CSF pressure [3]. CSF pressure from the lumbar region is classically measured by a manometer [4]. However, spinal manometer has some disadvantages in terms of the time required to obtain a correct CSF pressure and its cost. An alternative way of measurement is possible by calculation of flow rate of CSF through a spinal needle based on Poiseullie's law [5]. The Poiseullie's law which has the famous formula of ѵ=πpr4/8 ηL, describes laminar flow of a fluid a long a pipe (ѵ=flow rate; p=the pressure gradient between the two ends of the pipe; r=radius of the pipe; L=length of the pipe η=the viscosity of the fluid). We employed a new technique based on CSF drop-rate calculation grounded on Poiseullie's law [6]. Normal Cerebrospinal fluid Opening Pressure (COP) is 7-10 cm H2O in adults [7,8]. CSF pressure can change depending on the body position [4]. Flexed and relaxed body position of the patient during Lumbar Puncture (LP) is an important determining factor for the correct COP measurement such that COP in flexed position can lead to over-diagnosis of increased COP [1,4]. CSF is produced from the choroid plexus cells at a rate of 0.4 ml/min in adults [9]. With the use of Magnetic Resonance Imaging (MRI), it was shown that CSF flow is pulsatile [10]. In cranio-caudal direction CSF flow is 0.77 ml/min and in caudo-cranial direction CSF flow is 0.41 ± 0.51 ml/min [11]. CSF flow depends on the pulsation of the plexus arterials. CSF flows from the lateral ventricles to the third and fourth ventricle and the basal cisterns [8,12,13]. Then, CSF flows through the subarachnoid space. CSF is mainly absorbed through the subarachnoid space of the cranial nerves that invade eyes and the nose. CSF is also absorbed from the spinal nerves, the cribriform plate and lymphatic system [14]. CSF is renewed four to five times, daily. Investigation of CSF has been limited due to its invasive nature. This problem hindered our knowledge on healthy patients in terms of their CSF pressure and the physicochemical properties of CSF. The disadvantages presented by the conventional spinal manometry are indicative of a need to use alternative time and costeffective methods. In this study, we hypothesized that CSF drop time intervals through a spinal needle can be used to predict CSF pressure with high accuracy and in shorter period of time. We present a novel device to measure CSF pressure as a need to overcome problems due to spinal manometer such as prolonged measurement time, infection risk and the cost of manometer.
Methods
Novel device
We present the prototype of a novel device with patent number 2017-GE-183403. The device we designed is composed of two parts: a drop sensor and a digital chronometer. The drop sensor is composed of an infrared receiver/transmitter where first and fourth CSF drops work as a shutter for the chronometer. First drop passing through the sensor starts the chronometer and the fourth drop passing through the sensor stops the chronometer.
The schematic of the device is depicted in Figure 1. The time interval between first and fourth drop was recorded for each pressure point in triplicate measurements for each type of spinal needle.
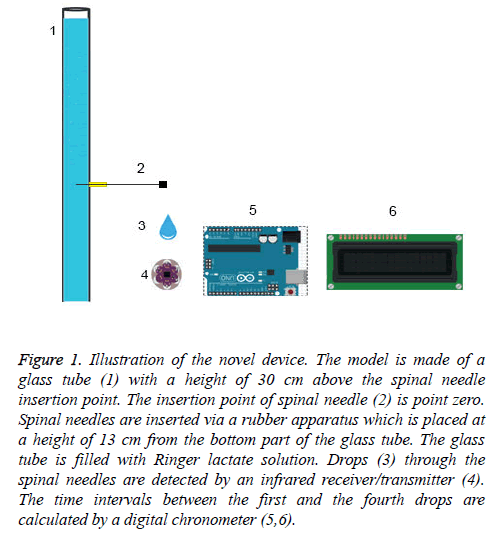
Figure 1: Illustration of the novel device. The model is made of a glass tube (1) with a height of 30 cm above the spinal needle insertion point. The insertion point of spinal needle (2) is point zero. Spinal needles are inserted via a rubber apparatus which is placed at a height of 13 cm from the bottom part of the glass tube. The glass tube is filled with Ringer lactate solution. Drops (3) through the spinal needles are detected by an infrared receiver/transmitter (4). The time intervals between the first and the fourth drops are calculated by a digital chronometer (5,6).
CSF model
This in vitro study was performed on a non-pulsatile CSF model (Figure 1). The model is made of a glass tube with a height of 30 cm above the spinal needle insertion point. The insertion point of spinal needle is point zero. Spinal needles were inserted via a rubber apparatus which was placed at a height of 13 cm from the bottom part of the glass tube. Ringer lactate solution was used as it was reported with optimum characteristics reflective of the CSF [15]. Our four-drop method which employs a non-pulsatile CSF model was compared with a pulsatile CSF model. The difference between the non-pulsatile and pulsatile CSF models was compared using 22 G, 25 G and 26 G quincke spinal needles.
Spinal needles
Spinal needles of 22 G quincke (M. Schilling), 22 G pencil point (Braun Spinocan), 25 G quincke (M. Schilling), 25 G pencil point (Braun Spinocan), 26 G quincke (M. Schilling), 26 G pencil point (Braun Spinocan), 27 G quincke (M. Schilling) were used to compose a reference table for a pressure range of 1-30 cm H2O. Before each measurement, each pressure level of cm H2O was adjusted using a classical manometer. Starting from 1 cm H2O pressure, the interval time of the first and fourth drops per cm H2O was monitored for each spinal needle up to 30 cm H2O. This process was performed in triplicates and a reference table was constructed by the mean of these repeated experiments for each condition (Supplementary Table 1).
Blind randomised test
Pressure results for each spinal needle were validated with computer-generated randomization using 10 random pressure points between 1 and 30 cm H2O. The test was performed by two examiners. First examiner adjusted the pressure points determined by the computer, and covered the glass tube with an aluminium foil. Then, using our novel device, the second examiner monitored the drop-time intervals in a blind manner for each random-selected pressure point. All experiments were performed in triplicates and the mean drop-time of the blind measurements was recorded. The pressure points were predicted from the recorded values using the reference pressure table for each spinal needle (Supplementary Table 1).
Statistical analysis
The mean of triplicate measurements were taken and the statistics used for comparison of these two methods was performed with Bland-Altman test followed by Deming II analysis. The analysis was performed within the 95% confidence interval [16,17]. The pulsatile and non-pulsatile CSF models were compared using Student’s t-test. The effect of density of CSF was analysed using Pearson’s correlation coefficient. Graphpad Prism 7 software trial version was used for all statistical analysis.
Results
Four-drop method is non-inferior to the conventional CSF manometry
It has been shown that our new method is non-inferior to the conventional CSF pressure measurement by manometry with a slope range of 0.9704-1.011 within 95% confidence interval (p<0.0001).
The precision of this new CSF pressure measurement method was tested via blind randomised test. The distribution of the data obtained from these blind tests were analysed with a Bland-Altman scatter plot (Figure 2a).
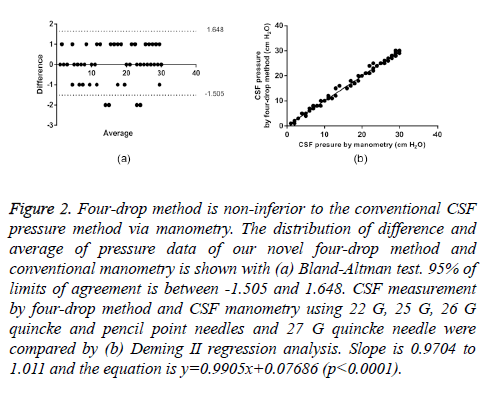
Figure 2: Four-drop method is non-inferior to the conventional CSF pressure method via manometry. The distribution of difference and average of pressure data of our novel four-drop method and conventional manometry is shown with (a) Bland-Altman test. 95% of limits of agreement is between -1.505 and 1.648. CSF measurement by four-drop method and CSF manometry using 22 G, 25 G, 26 G quincke and pencil point needles and 27 G quincke needle were compared by (b) Deming II regression analysis. Slope is 0.9704 to 1.011 and the equation is y=0.9905x+0.07686 (p<0.0001).
As seen in Table 1, there are two important points. First, the bias between the mean differences (0.07) and SD of bias (0.8) are within acceptable range. Second, %95 limits of agreement is between -1.5 and +1.6. In the scatter plot, there are four values at -2 that are outside of the limits of agreement. From clinical point of view, the interval of agreements defined by our Bland-Altman analysis is within acceptable limits (± 2 cm H2O CSF pressure).
| Bias | 0.07143 |
| SD of bias | 0.8044 |
| 95% limits of agreement | |
| From | -1.505 |
| To | 1.648 |
Table 1. Bland-Altman analysis of four-drop method and CSF manometry.
Since normal distribution of the data was observed in Bland- Altman scatter plot, statistical analysis was followed by Deming II regression method. As indicated in the equation (y=0.9905x+0.07686), the two methods are highly similar (Table 2, Figure 2b). From the slope value (0.9905), a good overall concurrence between the two methods was observed.
| 95% confidence interval | |
| Slope | 0.9704 to 1.011 |
| y-intercept when x=0, 0 | -0.2915 to 0.4453 |
| p value | <0.0001 |
| Equation | y=0.9905x + 0.07686 |
Table 2. Deming II regression analysis of four-drop method and CSF manometry.
Although the readings obtained by the new method is very similar to the conventional manometry, for large-diameter spinal needles (22 G), the time intervals corresponding to the pressure range of 18-30 cm H2O were in close range (Supplementary Table 1). For instance, for 23 cm H2O, 24 cm H2O and 25 cm H2O pressure levels, the time intervals measured by the chronometer was 9.9 s, 9.8 s and 9 s, respectively. In order to measure these range of pressures with large-diameter needles, it is appropriate to use a special design chronometer to obtain an accurate pressure measurement.
For small-diameter needles such as 26 G quincke and pencil point; and 27 G quincke needle, the time intervals corresponding to 1-15 cm H2O were highly distinct. For 27 G quincke needle, the time intervals for 5-1 cm H2O were 326.6 s, 383.1 s, 491.4 s, 638.8 s and 1047.7 s, respectively. The time interval was approximately 17 min (1047.7 s) for the fourth drop corresponding to 1 cm H2O.
The pulsatile and non-pulsatile CSF models are indifferent with the use of novel four-drop method
The results indicated above were obtained using a non-pulsatile CSF model. CSF is a dynamic fluid with to-fro fashion (backward and forward movement of the fluid) such that it displays a pulsatile movement.
We tested four-drop method using a pulsatile set-up. The pulsatile set-up was constructed by connecting the CSF model to a medical ventilator as reported by Ginosar et al. [2]. To do this, we compared 22 G, 25 G and 26 G quincke needles in pulsatile and non-pulsatile CSF models. From the point of view of four-drop method, there is no difference between pulsatile and non-pulsatile models (p>0.05, student’s t-test).
The pressure can be easily adjusted in non-pulsatile systems. As this is not an easy procedure in pulsatile systems, researchers usually select one or two pressure points in their pulsatile CSF model [2].
Similarly, we chose a single pressure point to compare our non-pulsatile four-drop method in pulsatile condition. 22 G, 25 G and 26 G quincke spinal needles were used at pressure level of 30 cm H2O. The results are indicated in supplementary Table 2. For each spinal needle type, there was no significant difference between time intervals.
Novel four-drop method is not affected by CSF density
Time intervals of 22 G, 25 G and 26 G quincke needles in nonpulsatile four-drop CSF model filled with mannitol 20 % were measured in triplicates for pressure range of 1-30 cm H2O. These data were compared with the corresponding Ringer lactate data using Pearson’s correlation analysis (Supplementary Figure 1). R square was 0.9864 for 22 G, 0.9707 for 25 G and 0.9553 for 26 G needles with p<0.0001 for all conditions within 95% confidence interval.
Discussion
We have shown for the first time that the interval between first and fourth consecutive drops of CSF from a spinal needle is reflective of the opening CSF pressure. The first and fourth drop of CSF is an indirect means to measure COP.
CSF pressure has been of interest of clinicians for different reasons. While neurologists and paediatricians use CSF pressure for diagnostic LP, anaesthetists use CSF pressure for investigation during spinal anesthesia [18]. The correct measurement of COP is essential for many conditions such as cerebral infection diseases and traumatic brain injury [19]. However, there are several constraints to measure COP accurately.
First, spinal manometer-related errors compromise this measurement [20]. Second, the gauge of the spinal needle used during LP is determining factor of correct CSF pressure measurement. Third, the density of CSF influences accurate COP [21]. We have devised a novel method which overcomes all of these caveats. Elimination of these points via our new method will be further discussed from these perspectives.
Our novel method which is grounded on Poiseullie's law by measuring the time between the first and the fourth consecutive drops of CSF from a spinal needle, is not influenced by these disrupting conditions such as CSF density and the spinal needle gauge [6].
Classical method to measure COP with a spinal manometer has several disadvantages. There is conflicting data for the time required to measure CSF pressure (equilibration time) with a manometer [2,22]. Equilibration time is the time required for the CSF to reach to the top most level in the manometer. Carson and colleagues have reported measurement of "equilibration time" using 20 G spinal needle is over 30 s with90 % success. The 90% success is defined by Carson et al. as showing minimum 90% of the true CSF pressure in under 1 min [22]. However, for 22 G quincke needle the equilibration time goes over 120 s and for 25 G quincke over 180 s, with at most 65% success. Therefore, for needles smaller than 20 G, the time required to measure CSF pressure is over 2 min only reflecting 65% of the true CSF pressure. For instance, if the patients CSF pressure is 10 mmH2O, with 22 G needle at 120 s the value on the manometer will read 6.5 mmH2O according to Carson et al. However, in Ginosar et al.’s findings, 22 G quincke spinal needle has ”equilibration time” of 40,7 seconds which is much shorter compared with Carsons' results [2,22].
Although, Ginosar et al. attributed this dramatic difference to the pulsatile model they employed, instead of the non-pulsatile model used by Carson et al.; there may be other factors for this difference. For instance, the different equilibrium times reported by these groups can be due to the type of manometer they used which have a different dead space. Dead space is defined as the inner volume of a manometer per cm height. Dead space is one of the most important factors that influence the “equilibration time” of the CSF pressure measurement.
The time required for the fluid to reach to the top most level in the manometer “equilibration time” is directly proportional to the inner volume of the manometer (dead space) as indicated in the following formula, Q (flow rate)=volume (dead space)/time (equilibration time ).
Carson et al. used a manometer which has dead space of 0.05 ml of CSF per measured height. On the other hand, Ginosar et al. did not indicate the dead space of the manometer they used. From their equilibration time data, it can be inferred that their manometer had a smaller dead space. Any one fold increase in the dead space leads to one fold increase in the “equilibration time”.
The time required to measure CSF pressure and the type of spinal needle used for this procedure is highly variable in different study groups. These variations indicate the need to optimize a robust and reliable method for the CSF pressure measurement other than spinal manometry. Our method is reliable and shortens the time required dramatically for CSF pressure measurement time.
Spinal needle related errors
Carson et al. has reported that spinal needles with gauge less than 22 G are not suitable for measurement of CSF pressure in an acceptable “equilibration time” [22]. However, Ginosar et al. reported that 22 G shaft with tapered and 27 G pencil point spinal needles have similar characteristics as of 22 G quincke spinal needle in terms of their “equilibration time” [2].
The variability of the equilibrium time reported by these groups indicates the need to optimize a robust and reliable method for the CSF pressure. The inconsistency of the "equilibration time" reported by different groups show that "equilibration time" is not a suitable method to measure CSF pressure accurately. Therefore, the time required to measure CSF pressure and the type of spinal needle used for this procedure is highly variable in different study groups. Our method is reliable and shortens the time required dramatically for CSF pressure measurement time.
The flow rate of CSF through the spinal needles depends on their gauge and design characteristics. Spinal needles manufactured by different companies may differ in their inner diameters therefore they can have different flow rates. For instance, a 27 G spinal needle is expected to have smaller inner diameter than a 26 G spinal needle. Contrary to this assumption, Spinocan 26 G needle has an inner diameter (0.22 mm ) which is smaller than the inner diameter of Beckton and Dickinson 27 G spinal needle (0.27 mm).
Venkatesh et al. worked on the effect of the gauge, length and design of spinal needles on COP and found that needles with small gauge and long length have extended COP [23]. Zorrilla- Vaca et al. compared the cutting and pencil point needles in terms of PLPH with the different patients of 5631 patients, including 22 studies [24]. There was a significant difference between the needle gauge and the PLPH in the cutting needles, but not in the pencil points.
CSF density depended errors
Cerebrospinal fluid is an active compound is not just a simple ultra-filtrate of plasma. It's a carrier of ions and molecules with low levels of urea and protein and with high levels of Cl- and Mg++. 99% of CSF is composed of water while 92% of the plasma.
Central Nervous System (CNS) disease disrupt the CSF biochemistry. The density of CSF is 1.0003 g/ml (± 0.0003) at 37°C [25]. The density of fluids changes upon heat with increments (i. e., the density of water is 1.000 g/ml at 37°C and 0.9934 g/ml at 4°C [26]. Cerebrospinal fluid density has been calculated in several CNS disease with the highest density level reported as 1.005 g/ml for a patient with diabetes and convulsion disease [27].
Instead of serum physiologic% 0,9 (density 1.005-1.006 g/ml at 20°C) or mannitol 20% (density 1.07 g/ml); Robinson et al. used ringer lactate (density 1.005 g/ml) in their model and indicated that this solution has the optimum characteristics resembling CSF [15]. The "equilibration time" changes upon use of these solutions with a range of density values [2]. In the light of these findings, the effect of solutions with different densities was tested on the four-drop method with comparison of ringer lactate and mannitol 20%. Employing our four-drop method, we found a high correlation between ringer lactate and mannitol 20% solutions. With these findings, we have overcome the effect of density variations.
Choosing CSF model type
In this study, the choice of CSF model type was of importance. CSF circulation with to-fro movements is classically known as third circulation [11,28,29]. The ease of pressure adjustment in non-pulsatile system is an advantage for this type of CSF model [30]. But, using a non-pulsatile CSF model is disadvantageous when modelling the pulsatile CSF movement. In pulsatile CSF models, the difficulty of pressure level adjustment compelled the researchers to concentrate their measurements on a single or double pressure level [2,22]. In our novel device, the need to construct a reference table a pressure level from 1 cm H2O to 30 cm H2O was measured in terms of fourth drop time interval. If a pulsatile CSF model was chosen, it would not be possible to accurately adjust 30 different pressure levels. Nevertheless, our four-drop method was shown to be indifferent in pulsatile and non-pulsatile CSF models.
Limitations
Efforts have been made to reduce the limitations in this study. The measurements were standardized with respect to the needle gauge that is the outer diameter of the needles. However, the outer diameter of the needles can be misleading for the inner diameter size which can change in different brand types.
The measurements in our non-pulsatile four-drop method were carried at room temperature. Therefore, the solution in the model was lower than the body temperature which can affect its density. However, the effect of this density variation is negligible in our four-drop method [25].
CSF pressure may influence the PLPH prevalence. In future studies, clinicians may focus on the effect of CSF pressure on the PLPH using the practical four-drop method. Our four-drop method may help the clinicians to take precautions in this situation.
Conclusion
The novel device presented in this study has the data for only seven different spinal needle types and a reference table. The device can be developed further with detailed spinal needle parameters such as the brand types and inner diameter information and an uploaded reference table.
In conclusion, we have developed an alternative method to measure CSF pressure with high accuracy. The four-drop method is non-inferior to the classical spinal manometry with its time and cost-effective benefits.
Authors’ Contributions
Study design: FU and DY; Data collection and analysis: FU and DY; Writing the first draft of the manuscript: FU and DY.
Declaration of Interest
None declared.
References
- Bradley KC. Cerebrospinal fluid pressure. J Neurol Neurosurg Psych 1970; 33: 387-397.
- Ginosar Y, Smith Y, Ben-Hur T, Lovett JM, Clements T, Ginosar Y D, Davidson EM. Novel pulsatile cerebrospinal fluid model to assess pressure manometry and fluid sampling through spinal needles of different gauge: support for the use of a 22 G spinal needle with a tapered 27 G pencil-point tip. Br J Anaesth 2012; 108: 308-315.
- Khlebtovsky A, Weitzen S, Steiner I, Kuritzky A, Djaldetti R, Yust-Katz S. Risk factors for post lumbar puncture headache. Clin Neurol Neurosurg 2015; 131: 78-81.
- Sithinamsuwan P, Sithinamsuwan N, Tejavanija S, Udommongkol C, Nidhinandana S. The effect of whole body position on lumbar cerebrospinal fluid opening pressure. Cerebrospin Fluid Res 2008; 5: 11.
- Boyles TH, Gatley E, Wasserman S, Meintjes G. Brief report: flow rate of cerebrospinal fluid through a spinal needle can accurately predict intracranial pressure in cryptococcal meningitis. J Acqu Immune Defic Syndr 2017; 74: 64-66.
- Pfitzner J. Poiseuille and his law. Anaesthesia 1976; 31: 273-275.
- Di Ieva A, Schmitz EM, Cusimano MD. Analysis of intracranial pressure: past, present, and future. Neurosci Rev j Neurobiol Neurol Psych 2013; 19: 592-603.
- Johanson CE, Duncan JA, Klinge PM, Brinker T, Stopa EG, Silverberg GD. Multiplicity of cerebrospinal fluid functions: New challenges in health and disease. Cerebrosp Fluid Res 2008; 5: 10.
- Rubin RC, Henderson ES, Ommaya AK, Walker MD, Rall DP. The production of cerebrospinal fluid in man and its modification by acetazolamide. J Neurosurg 1966; 25: 430-436.
- Ridgway JP, Turnbull LW, Smith MA. Demonstration of pulsatile cerebrospinal-fluid flow using magnetic resonance phase imaging. Br J Radiol 1987; 60: 423-427.
- Brinker T, Stopa E, Morrison J, Klinge P. A new look at cerebrospinal fluid circulation. Fluids Barriers CNS 2014; 11: 10.
- Bradley WG, Haughton V, Mardal KA. Cerebrospinal fluid flow in adults. Handb Clin Neurol 2016; 135: 591-601.
- Johanson CE. Choroid Plexus-cerebrospinal fluid circulatory dynamics: impact on brain growth, metabolism, and repair. Neurosci Med Hum Press Totowa NJ 2008; 173-200.
- Johnston M, Zakharov A, Koh L, Armstrong D. Subarachnoid injection of Microfil reveals connections between cerebrospinal fluid and nasal lymphatics in the non-human primate. Neuropathol Appl Neurobiol 2005; 31: 632-640.
- Robinson RA, Stewart SF, Myers MR, Lien LF, Rinaldi JR, Swisher JL, Drasner K. In vitro modeling of spinal anesthesia. A digital video image processing technique and its application to catheter characterization. Anesthesiology 1994; 81: 1053-1060.
- Kaul S, Diamond GA. Good enough: a primer on the analysis and interpretation of noninferiority trials. Ann Int Med 2006; 145: 62-69.
- Walker E, Nowacki AS. Understanding equivalence and noninferiority testing. J Gene Int Med 2011; 26: 192-196.
- Kleyweg RP, Hertzberger LI, Carbaat PA. Significant reduction in post-lumbar puncture headache using an atraumatic needle. A double-blind, controlled clinical trial. Cephalalgia Int J Headache 1998; 18: 635-637.
- Jackson A, Hosseinipour MC. Management of cryptococcal meningitis in sub-saharan Africa. Curr HIV/AIDS Rep 2010; 7: 134-142.
- Allen R. Intracranial pressure: a review of clinical problems, measurement techniques and monitoring methods. J Med Eng Technol 1986; 10: 299-320.
- Greene NM. Distribution of local anesthetic solutions within the subarachnoid space. Anesth Analg 1985; 64: 715-730.
- Carson D, Serpell M. Choosing the best needle for diagnostic lumbar puncture. Neurology 1996; 47: 33-37.
- Bellamkonda VR, Wright TC, Lohse CM, Keaveny VR, Funk EC, Olson MD, Laack TA. Effect of spinal needle characteristics on measurement of spinal canal opening pressure. Am J Emerg Med 2017.
- Zorrilla-Vaca A, Healy R, Zorrilla-Vaca C. Finer gauge of cutting but not pencil-point needles correlate with lower incidence of post-dural puncture headache: a meta-regression analysis. J Anesth 2016; 30: 855-863.
- Horlocker TT, Wedel DJ. Density, specific gravity, and baricity of spinal anesthetic solutions at body temperature. Anesth Analg 1993; 76: 1015-1018.
- Higuchi H, Hirata J, Adachi Y, Kazama T. Influence of lumbosacral cerebrospinal fluid density, velocity, and volume on extent and duration of plain bupivacaine spinal anesthesia. Anesthesiology 2004; 100: 106-114.
- Davis H, King WR. Densities of cerebrospinal fluid of human beings. Anesthesiology 1954; 15: 666-672.
- Scalzo F, Bergsneider M, Vespa PM, Martin NA, Hu X. Intracranial pressure signal morphology: real-time tracking. IEEE Pulse 2012; 3: 49-52.
- Nitz WR, Bradley WG, Watanabe AS, Lee RR, Burgoyne B, Osullivan RM, Herbst MD. Flow dynamics of cerebrospinal fluid: assessment with phase-contrast velocity MR imaging performed with retrospective cardiac gating. Radiology 1992; 183: 395-405.
- Gil F, Garcia-Aguado R, Barcia JA, Guijarro E, Hostalet F, Tommasi-Rosso M, Grau F. The effect of fibrin glue patch in an in vitro model of postdural puncture leakage. Anesth Analg 1998; 87: 1125-1128.