ISSN: 0970-938X (Print) | 0976-1683 (Electronic)
Biomedical Research
An International Journal of Medical Sciences
Research Article - Biomedical Research (2018) Computational Life Sciences and Smarter Technological Advancement: Edition: II
A prediction model for type 2 diabetes using adaptive neuro-fuzzy interface system
DOI: 10.4066/biomedicalresearch.29-17-254
Visit for more related articles at Biomedical ResearchDiabetes has become a major threat to the life and it is getting common day by day and is having a fast increasing trend .Unhealthy practices in consumption of food have on a major side contributed to the rise of type 2 diabetes. In this paper we have tried to develop a method for the prediction of type 2 diabetes using adaptive neuro-fuzzy interface system (ANFIS) with genetic algorithms (GA). A comparative study has also been done with the result of our previous work in which General Regression Neural Network (GRNN) is applied.
Keywords
Diabetes, ANFIS, Bioinformatics, Prediction, Data mining.
Introduction
During the last decade, medical field witnessed a tremendous development in research. An immeasurable amount of data was created as a result of various research and studies. The need to study, analyze and make sense out of these data lead to the new inter-discipline Bioinformatics. Bioinformatics combines computer science, mathematics, statistics and engineering to interpret and analyze biological data. A lot of research and studies were done in this field during the recent past which has resulted in evolution of new theories and uncontrolled and highly distributed data. The necessity to segregate and process this wide variety of data has promoted to the research and development in Data Mining. Data cleaning and data integration methods developed in data mining will help the integration of bio-medical data and the construction of data warehouses for bio-medical data analysis [1]. In our research work we have tried to improve the accuracy of predicting diabetes using adaptive neuro-fuzzy interface system (ANFIS) with genetic algorithms (GA).
Diabetes Mellitus is one of the fatal diseases growing at a rapid rate in developing countries like India. Diabetes is the case in which the patient’s pancreas is unable to generate sufficient insulin or else the body is unable to utilize the insulin produced effectively. There are three types of diabetes. Type 1 diabetes, Type 2 diabetes and Gestational diabetes [2].
Among these 3 types, type 2 diabetes is taken into consideration for our work. Recent research shows that the main cause of type 2 diabetes is the obesity and sedentary lifestyle which may affects the genetic elements [3]. Both male and female in any age group has chance for diabetes. Diabetes can be especially hard on women. The burden of diabetes on women is unique because the disease can affect both mothers and their unborn children [4].
This paper is organized as follows: Section 2 describes the dataset which is used for this study, the detailed analysis among each age group and the method used for this study. The results obtained by our proposed system and a comparison with the method which is used in our previous work and the other methods used by many researchers in recent past are given in section 3.
Material and Method
Dataset
The Pima Indian dataset is used throughout the research work. In this dataset the female at least 21 years old is taken into consideration. 768 instances with 8 parameters have been considered. The parameters are:
1. Number of times pregnant
2. Plasma glucose concentration a 2 hours in an oral glucose tolerance test
3. Diastolic blood pressure
4. Triceps skin fold thickness
5. 2-hour serum insulin
6. Body mass index
7. Diabetes pedigree function
8. Age
Among these, the number of times pregnant, BMI and age can easily be found by the people without any clinical tests. So in this study we analyzed these 3 parameters in detail. The total 768 entries are classified into 4 groups according to their age like 20-30, 30-40, 40-50 and 50 above. In first group there are 397 entries among them only 84 instances are positive i.e. 21%. In the other groups almost 50% of the instances are positive. This shows increase in age results in increase in the possibility to have diabetes (Figures 1-3).
From the above graphs it is observed that in the age group of 20-30, the chance of repeated pregnancy is very less. Here high BMI is one of the main causes to have diabetes. In the next two groups more no of pregnancy plays a vital role in having diabetes. Again in the age group from 50 and above, increased BMI leads to the possibility of becoming diabetic.
Adaptive network based fuzzy inference system (ANFIS)
Concept and structure: ANFIS is a combination of the intelligent approaches in neural network and fuzzy logic in order to obtain a good reasoning in quality and quantity. Thus the network obtained via fuzzy logic has extra ordinary capacity of training by virtue of neural networks and linguistic interpretation of variables. The both of them encode the information in parallel and distribute architecture in a numerical framework.
Rule: if x is A1 and y is B1 then f (x) = px + qy + r → (1)
Where x and y are the inputs, A and B are the fuzzy sets, f are the output, p, q and r are the design parameters that determined during the training process. ANFIS consists of two sections.
• Antecedent
• Conclusion
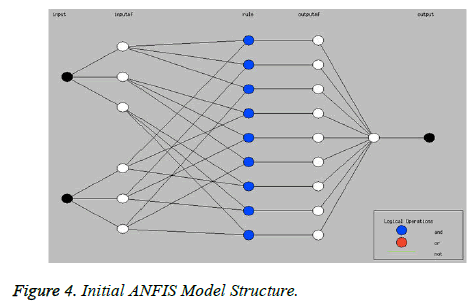
These two are linked with each other in the form of networks. This network is constructed using five layers and each of this layer is having several nodes. Fig.4 explains the structure of the same.
layer 1: executes a fuzzification process which denotes membership functions (MFs) to each input. In this paper we choose Gaussian functions as membership functions:
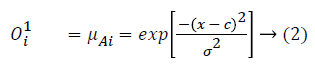
layer 2: executes the fuzzy AND of antecedents part of the fuzzy rules
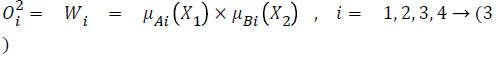
layer 3: normalizes the MFs
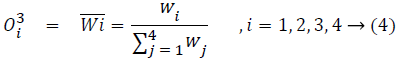
layer 4: executes the conclusion part of fuzzy rules
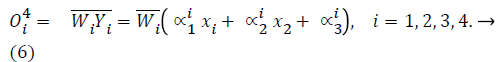
layer 5: computes the output of fuzzy system by summing up the outputs of the fourth layer which is the de-fuzzification process.
Learning Algorithm
In ANFIS, membership function parameters of
1. each input
2. the consequents parameters
3. number of rules
4. are tuned.
nbr_rule = mn → (7)
Here n indicates number of inputs and m is the number of membership functions by input. All the possible rules are generated by these functions.
Different levels of training are required for this. Namely:
Structure learning: This allows in finding out the required structure of network, which is the relevant partitioning of the input space.
Parametric learning: This learning is carried out for adjusting the membership functions and consequent parameters.
In almost all systems the structure is finalized by experts in this area. In this work we tried for a combination of both of the above learning structures.
For obtaining an optimal set of rules and for learning rules, number of methods have been devised subsequent to the development of ANFIS approach.
Hybrid learning is the most commonly used training algorithm. This is carried out in two steps:
• Forward pass
• Backward pass I
In forward pass whenever all the parameters are initialized, functional signals go forward till fourth layer and the consequents parameters are identified by LSE. After identifying consequents parameters, the functional signals keep going forward until the error measure is calculated. In the backward pass, the error rates bounce backward and the premise parameters are rationalized by gradient decent.
The function to be minimized is Root Mean Square Error (RMSE):
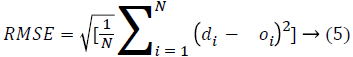
Where di is the desired output and Oi is the ANFIS output for the ith sample from training data and N is the number of training samples [5].
Algorithm: Adaptive Neuro-Fuzzy Inference System Genetic Algorithm (ANFISGA).
This method is based on Neuro-fuzzy inference system and genetic algorithm.
In ANFISGA there are eight inputs and one output.
In ANFISGA we have five layers.
Layer 1 is the input layer. Neurons in this layer simply pass external crisp signal to Layer 2. Layer 2 is the fuzzification layer. Neurons in this layer perform fuzzification.
Layer 3 is the rule layer. Each neuron in this layer corresponds to signal Sugeno-type fuzzy rule.
Layer 4 is the normalization layer. Each neuron in this layer receives inputs from all neurons in the rule layer, and calculates the normalized firing strength of given rule.
Layer 5 is the defuzification layer. Each neuron in this layer is connected to the respective normalization neuron.
The general process of this algorithm is summarized in the following steps
Step 1. Parameter setting: Genetic Algorithm has some key factors which effect significantly the algorithm performance. The parameters namely number of times pregnant, plasma glucose concentration, diastolic blood pressure, skin fold thickness, insulin level, body mass index, pedigree function, missing attribute value rates are determined in this step.
Step 2. Initialization: In an initial solution current solution S is selected randomly. Then a collection of mutations is randomly done on the solution to generate new temporary solutions.
Step 3. Weight generation: In this step, the weights are created and evaluated individually to organize the input parameters.
Step 4. Sort: The weights are sorted in descending order based on their fitness values. Therefore, the most common and effective experiences are placed on the top.
Step 5. Selection: In this step, the input parameters with high fitness values are randomly selected.
Step 6. Evaluation: If the optimality condition is satisfied for the new solution S', then new weight is generated. The new weights with fitness value are replaced with the worst experience in the input parameters.
Step 7. Repeat: If the stopping criterion is not satisfied, the above steps are repeated consecutively; otherwise the current solution is returned as the output of the input parameters.
Working of ANFIS
The architecture and learning procedure underlying ANFIS (Adaptive Network- based Fuzzy Inference System) is presented, which is a fuzzy inference system implemented in the framework of adaptive networks.
The proposed ANFIS uses a hybrid learning procedure, which can construct an input-output mapping based on stipulated input-output data pairs and human knowledge (in the form of fuzzy if-then rules) .
Building the model: The model is build, by creating, training, and testing Adaptive Network-based Fuzzy Inference System (ANFIS). The following tasks were performed (Figure 4):
• Data pre-processing
• Loading the data
• Generating the Initial ANFIS Structure
• Training the ANFIS
• Validating the Trained ANFIS
Data pre-processing: In this step we are randomly generating training data and testing data in the Input Pima Dataset for analyzing the results.
Loading the data: The first step in training the ANFIS is loading the data set which contains the desired input/output data of the model which is considered.
The structure of the data set to be loaded must be an array in which data is arranged in column vectors and the last column with output data. We also loaded Testing data.
Generating the Initial ANFIS Structure: Before we starting the ANFIS Training we are generating the Initial ANFIS Structure as shown below.
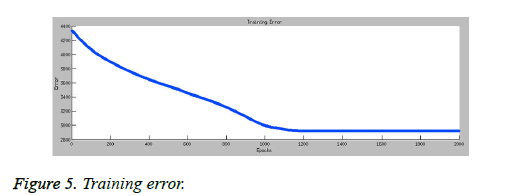
Training the ANFIS: After loading the training data and generating the initial ANFIS structure, we started training the ANFIS. The number of training Epochs (Epochs means number of iterations) is over 1000. During training we can see how Training error develops as given in Figure 5.
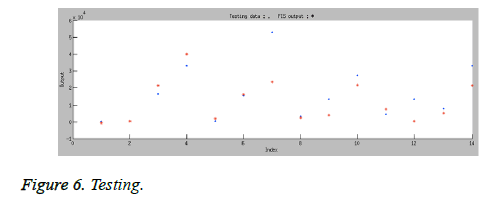
Validating the Trained ANFIS: Finally, we had to test our data against the trained ANFIS. After the ANFIS is trained, validate the model using a testing data that differs from the one we used to train the ANFIS. When we test the testing data against the ANFIS, it looks satisfactory (Figure 6).
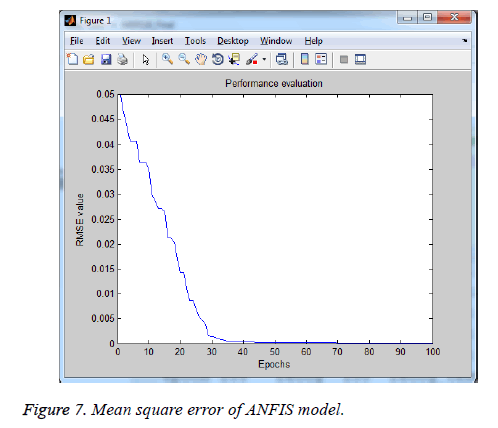
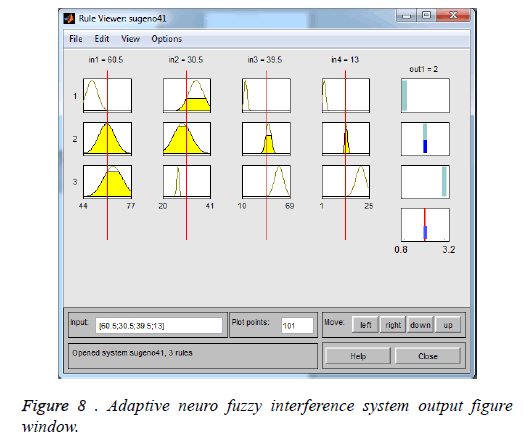
The results indicate that the ANFIS model has a minimum Mean Square Error (MSE) (Figure 7). The Figure 8 shows the output window for input and output obtained using ANFIS after training input data.
Results and Discussion
Using ANFIS with GA we got an accuracy of 93.49% in the training and 96.08% in the testing. In our previous work we have used General Regression Neural Network (GRNN) for the prediction. Generalized Regression Neural Networks and Adaptive Neuro Fuzzy Interference System are popular data modeling tools that can perform intelligent tasks similar to the human brain. Both Generalized Regression Neural Networks and fuzzy systems are very adaptable in estimating the input– output relationships. Some uncertainties are bound to arise at many stages of data classification system. This is mainly because of indefiniteness in defining features, ambiguity or vagueness in input data presence of imprecise input information and overlapping boundaries among classes. The Adaptive Neuro Fuzzy Interference System as a generalization of the classical set theory is very flexible in handling different aspects of uncertainties or incompleteness about real life situations.
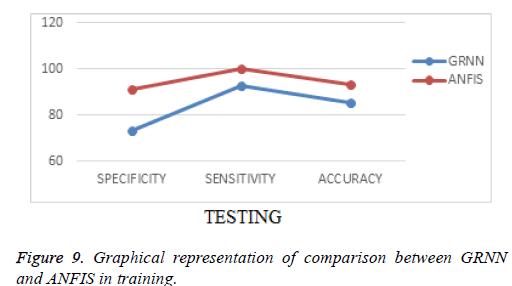
Generalized Regression Neural networks deal with numeric and quantitative data whereas Adaptive Neuro Fuzzy Interference System can handle symbolic and qualitative data. Neuro-fuzzy hybridization leads to a crossbreed intelligent system widely known as Neuro-fuzzy system that exploits the best qualities of these two approaches efficiently. The hybrid system unites the human alike logical reasoning of fuzzy systems with the learning and connectedness structure of neural networks by means of Adaptive Neuro Fuzzy Interference System based approach. The Figure 9 and Table 1 show the comparison between the results of GRNN and ANFIS during training.
| Training | |||
|---|---|---|---|
| Specificity | Sensitivity | Accuracy | |
| GRNN | 73.35 | 91.45 | 85.49 |
| ANFIS | 91.35 | 100 | 93.49 |
Table 1. Comparison between the results of GRNN and ANFIS during training.
• Sensitivity = specificity and accuracy are described in terms of TP, TN, FN and FP [6].
• Sensitivity = TP/(TP + FN) = (Number of true positive assessment)/(Number of all positive assessment)
• Specificity = TN/(TN + FP) = (Number of true negative assessment)/(Number of all negative assessment)
• Accuracy = (TN + TP)/(TN+TP+FN+FP) = (Number of correct assessments)/Number of all assessments)
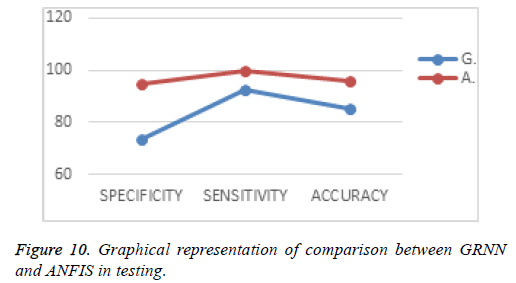
The Figure 10 and Table 2 show the comparison between the results of GRNN and ANFIS during the testing.
| Specificity | Sensitivity | Accuracy | |
|---|---|---|---|
| GRNN | 73.35 | 92.63 | 85.49 |
| ANFIS | 94.82 | 100 | 96.08 |
Table 2. Comparison between the results of GRNN and ANFIS during testing.
In a study, Kayaer and Yıldırım [7] have used GRNN and got 80.21% accuracy. In study by Polat and Gunes [8] have applied ANFIS with PCA on the task of diagnosing diabetes disease and an accuracy of 89.47% was obtained. The proposed method was arrived highest among these two.
Conclusion
In the research presented in this paper, ANFIS with GA was applied for predicting diabetes disease and the most accurate result was obtained compared to our previous work in which we have tried the same using GRNN. The results strongly suggest that ANFIS with GA can aid in the field of diabetes disease. The most widely used approach for numeric prediction is regression, a statistical methodology. Optimization technique like Genetic Algorithm has much more influence on the accuracy of classification techniques. A combination of ANFIS and GA gave better results than the results achieved by using GRNN. It is hoped that more remarkable results will follow on further investigation of data. For the purpose of efficiently tuning of ANFIS parameters, any other suitable optimization technique like Particle Swarm Optimization (PSO) or Mine Blast Algorithm (MBA) could be combined with ANFIS.
References
- Han J. How Can Data Mining Help Bio-Data Analysis? BIOKDD-2002, 2nd Workshop on Data Mining in Bioinformatics, July 2002.
- Alby S, Shivakumar BL. A Prediction Model for Type 2 Diabetes Risk among Indian Women. ARPN J Eng Appl Sci 2016.
- Shivakumar BL, Alby S. A Survey on Data-Mining Technologies for Prediction and Diagnosis of Diabetes. Int Conf Intell Comput Appl (ICICA) 2014.
- Bar-Cohen Y. Biologically Inspired Intelligent Robots Using Artificial Muscles. Strain 2005; 41: 19-24.
- Jang JSR. ANFIS: Adaptive Network Based Fuzzy Inference Systems. IEEE Trans Syst Man Cybernet 1993; 23: 665-685.
- Zhu W, Zeng N, Wang N. Sensitivity, Specificity, Accuracy, Associated Confidence Interval and ROC Analysis with Practical SAS® Implementations. NESUG, 2010.
- http://www.rjpbcs.com/pdf/2016_7(2)/[131].pdf
- Polat K, Gunes S. An expert system approach based on principal component analysisand adaptive neuro-fuzzy inference system to diagnosis of diabetes disease. J Digital Signal Process 2007; 17: 702-710.