ISSN: 0970-938X (Print) | 0976-1683 (Electronic)

Biomedical Research

An International Journal of Medical Sciences

Research Article - Biomedical Research (2017) Volume 28, Issue 19

Effect of load on shear wave speed in muscle

Xiao Chen1,2*, Qianyi Ji1 and Chang Xu1

1School of Electronic and Information Engineering, Nanjing University of Information Science and Technology, Nanjing, PR China

2Jiangsu Key Laboratory of Meteorological observation and Information Processing, Nanjing University of Information Science and Technology, Nanjing, PR China

*Corresponding Author:
Xiao Chen
School of Electronic and Information Engineering
Nanjing University of Information Science and Technology, PR China

Accepted on December 21, 2017

Visit for more related articles at Biomedical Research

Abstract

It is difficult to detect muscle tension in vivo. In vitro experiments, the young's modulus of human muscle changes with the tension and the shear wave speed is affected by young’s modulus. The tension can be qualified by using the shear wave elastography method. In this paper, the hyperelasticity model for muscles was established. The shear wave speeds in the muscle tissues under tension were studied by applying different statistic loads in the axial direction, and the effect of loads on the shear wave speeds was obtained. The results show that the shear wave speeds increases from 6.1 m/s to 13.1 m/s as the load increases from 0 to 50 kpa, and the speed is linearly related to the load. The shear wave elastography method could be used as a potential non-invasive method to measure the tension in tissues.

Keywords

Hyperelasticity, Shear wave elastography, Shear wave speed, Muscle.

Introduction

Shear wave elastography (SWE) is a promising method of medical imaging. It is a new method of obtaining quantitative tissue elasticity data and is a developing variation of ultrasound imaging. As a supplement to traditional ultrasonic imaging methods [1], shear wave elastography is based on acoustic radiation force. Compared with other elastic imaging methods, SWE is quantifiable, repeatable and noninvasive. It is found that the hardness, i.e., the Young’s modulus, of diseased tissues is different from the normal tissue. And the shear wave speed is greatly affected by Young's modulus [2]. Therefore, tissue lesions can be diagnosed by measuring the shear wave speed [2-4].

For organs, the load can usually be ignored. But the muscle is always in a state of stress in order to maintain physiological activities. Clinical and in vitro experiments show that the relative position of thick and thin filaments is different when the muscle is in the state of relaxation and contraction [5-7]. What’s more, detection data also show that the Young's modulus varies greatly under different load [5]. However, facing the difficulties in vivo detection, the specific distribution of force in muscle is not clear [6,7], and the theoretical model for muscle under load is imperfect. The emergence of shear wave elastic imaging technology can control the detection range flexibly by focus position. According to the relationship between the load and shear wave speed, the distribution of force in muscles can be obtained by measuring the shear wave speed. SWE has become a promising way of studying the distribution of force in muscles.

This article will discuss the establishment of a reasonable muscle model. Through the variation of shear wave speed caused by different loads, this paper provides the theoretical basis for studying the force distribution in vivo by using shear wave elastography.

Method

The principle of traditional elastic imaging is squeeze version of the device or addition low-frequency vibration, generating displacement. The Young's Modulus of the tissue can be obtained by comparing the strain before and after the deformation assuming that the muscle is linear elastic. σ=Eε, where σ is the stress, E is Young's modulus, and ε is strain [8]. But these methods need to be exposed to the surface of the tissue. They are not applicable to non-surface organs. With the development of technology, the introduction of acoustic radiation force enables the detection by controlling the focusing position, generating displacement and radiation shear wave [9] near the focus position. For linear elastic materials, the shear wave speed in the material can be expressed as

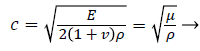equation (1)

Where c is linear elastic shear wave speed, ρ is the tissue density, v is Poisson's ratio, and μ is shear modulus.

It is shown that the linear elastic material model cannot meet the requirement of clinical trials, and there are obvious limitations. Therefore, a nonlinear model, such as viscoelasticity and hyperelasticity, is proposed for the muscle tissue.

The Ogden’s strain energy function model, one of the hyperelastic models, is better than other hyperelastic models, which is more suitable for fitting the stress hardening characteristics of nonlinear materials. The Ogden strain energy function is

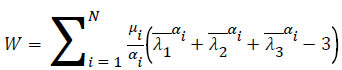
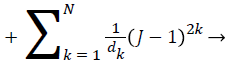equationequation (2)

Where W is a strain energy, and J is the compression ratio. 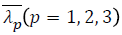equation is the Partial elongation ratio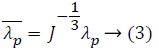equation

λp is the main elongation of three directions. For incompressible materials, J can be defined as 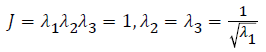equation

Results

As shown in Table 1, the shear wave speeds for the uniaxial tensile test data of isolated fox eye muscles [10] are compared with those calculated by using the Ogden model. To characterize the parameters in the Ogden model, the particle swarm optimization algorithm [11-13] was used. The Ogden strain energy equation of the N order can be written as

Elongation Experimental data of stress Simulation data of stress
1.06 1.20 1.19
1.15 8.31 8.56
1.24 18.09 23.01
1.33 31.18 35.15
1.42 47.71 54.77

Table 1. Uniaxial stretching experimental data and the Ogden model simulation data.

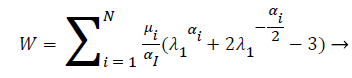equation (4)

The Ogden model includes two parameters, the shear modulus μ and the stress hardening coefficient α, which respond to the properties of the muscle tissue under the external stress. At the same elongation ratio, when the strain is small, the experimental data in vitro are close to the simulation results, and the experimental results are slightly lower than the simulation results as the strain increase. Table 2 shows the shear wave speeds under different loads. The result of the fitting of the applied stress and the corresponding speed is

Load (Kpa) Speed (m/s)
0 6.1233
1 6.3892
10 8.2336
20 9.6332
30 10.9157
40 11.9934
50 13.1172

Table 2. Shear wave speeds under different loads.

y=0.1391x+6.487 → (5)

Discussion

Beside the shape of the muscle model and the material parameters are set, the load and the constraint conditions of the model should be determined as well. The load is applied with two steps. The first step is the exertion of the external tension, the axial load is applied on the right section, and the load is gradually increased from 0 to 50 Kpa. The second step is to apply a sinusoidal excitation on a certain node in the middle of the model to generate the shear wave.

As the distance between the two nodes is small, the speed between the two adjacent nodes is simplified to a uniform motion when the speed of the shear wave is calculated. The farther the distance from the excitation node, the later the vibration appears, and the amplitude of the vibration decreases with the increase of distance. With the increase of the applied stress, the earlier the time of the wave peak of the displacement envelope of the same node shows that the shear wave speed increases with the increase of stress.

The time of flight (TOF) algorithm is used to calculate the shear wave speed. While there is no external load, the shear wave speed is about 6.1 m/s, and the speed increases with the increase of load. In the case of 50 kPa load, the speed reaches 13.1 m/s, and the specific speed change is shown in Table 2. There is a certain correlation between the tensile load and the shear wave speed, that is, the shear wave speed in the muscle tissue increases with the increase of the applied stress. The fitting result in Eq. (5) implies that the relationship between the applied load and the shear wave speed is basically linear.

Conclusion

In this paper, the hyperelasticity model is established and the linear relationship between the shear wave speed and the load is obtained by analyzing the shear wave spped in the muscle tissue. The results also show that shear wave elastography is feasible for detecting muscle force distribution in different states, which provides a basis for determining the distribution of force in vivo.

The cross sectional area, volume and hardness of the muscle tissue are affected by the individual conditions, such as sex, age, etc. The measured images maybe have noises and need denoise [14,15]. In addition, the model in this paper only considers the hyperelasticity of tissue. In fact, the muscle tissue is obviously viscoelastic. In the next stage, it is necessary to further optimize the muscle model and establish a more reasonable model.

Acknowledgement

This work was supported in part by project grants from the six talent peaks project in Jiangsu Province (DZXX-006), in part by 333 high level personnel training project Jiangsu Province of China, in part by the Natural Science Foundation of Jiangsu Province of China (BK20161536), and in part by the Priority Academic Program Development of Jiangsu Higher Education Institutions.

References