Biomedical Research

Abstract

Obstructive sleep apnea is a sleep related breathing disorder that occurs when the muscles relax during sleep, caused by the collapse of the soft tissues at the back of the throat and blocks the upper airway that increases the risk for several cardiovascular diseases. In this paper, a non-invasive method for screening patients with Obstructive Sleep Apnea (OSA) is proposed. The tracheal breath sound of the subjects was recorded in supine position, during wakefulness, and Hilbert Huang Analysis was performed. The differences between the output spectrums of OSA patients and other subjects enable the diagnosis of OSA with increased accuracy.

Keywords

Obstructive sleep apnea, Hilbert Huang transform, Diagnosis, Spectrum.

Introduction

Obstructive Sleep Apnea (OSA) is a common respiratory disorder and is caused by obstruction of the upper airway, which has the potential of becoming a lethal disease, if left untreated. Also, obstructive sleep apnea causes sleepiness during daytime, lack of concentration and snoring.

By definition, sleep apnea is the cessation of airflow to the lungs for at least 10 seconds during sleep. This is usually associated with more than 4% drop in oxygen saturation levels and so the supply of oxygen to all part of the body is less for OSA patients [1]. The likelihood of being affected with OSA increases with age and also it is more common among males than females because the structural and functional properties of upper airway are gender dependent [2].

Previous studies have shown that patients with OSA have a defective ability to dilate the pharynx during inspiration. Moreover, the tracheal breath intensity of people with OSA has been shown to increase significantly in supine position with respect to that of control group.

Currently, Polysomnography (PSG) during an entire night of patient’s sleep is the globally accepted standard diagnostic tool for sleep apnea. In a standard PSG procedure, ECG, EEG, EMG of chins, nasal airflow, EOG and abdominal movements are recorded.

PSG has a long waiting time and it requires night-long supervision and also it is an expensive test for health care system, neither portable nor convenient for patients. Like PSG, most of the existing diagnostic techniques of OSA are invasive, time consuming, costly and causing immense discomfort for the patient. To avoid all these inconveniences, we propose a new non-invasive and cost effective way of detecting Sleep Apnea using Hilbert Spectral Analysis (HSA).

The breathing sound of the subject is recorded during wakefulness in supine position. This is done using sensory audio recorder with the help of the software tool Audacity (Figure 1). Audacity is open source software which can be used by anyone without licensing.

Figure 1: Sensory audio recorder.

The recorded sound is then converted into signals by Audacity and is then fed into R_lab for Hilbert Spectral Analysis. At the end of the process, an output spectrum of the breathing signal is generated with which the presence of obstructive sleep apnea in the subject can be detected.

Sleep Apnea

Apnea literally means “Without Breathing”. Thus, sleep apnea refers to the condition in which breathing is stopped for a considerable amount of time during sleep [3]. This is a very common disease and is hardly diagnosed and treated. If left untreated, sleep apnea can cause severe breathing problems during sleep and may cause death of the person in sleep.

There are three main type of sleep apnea:

• Central apnea: Occurs because the brain does not send proper signal to the muscles that control the breathing.

• Obstructive apnea: Caused due to partial or complete block in airflow despite an on-going effort to breathe [4].

• Mixed apnea: Combination of central and obstructive apnea.

The severity of sleep apnea is assessed based on the value of Apnea-Hypopnea Index (AHI), which is the total number of apnea and hypopnea events per sleep hour. If the value of AHI is greater than 15 then it is moderate, and if the value is greater than or equal to 30 then the person suffer from severe sleep apnea [5].

Several factors have been recognized as risk factors of sleep apnea.c

• Sex: Males are more likely to be affected by sleep apnea than females. This could be attributed to the widespread differences in lifestyle between males and females.

• Age: The risk of getting sleep apnea increases with age. Sleep apnea is very common among adults older than the age of 65.

• High altitude: Sleeping at a higher altitude than normal increases the risk of sleep apnea. However, this is temporary and the problem disappears when the subject returns to the normal altitudes.

• Heart disorders: People with various types of heart diseases are more likely to develop sleep apnea. About 50% of people having congestive heart failure are affected by sleep apnea.

• Brain tumor: Brain tumors or strokes that alter the brain’s ability to regulate breathing may increase the risk of sleep apnea.

• Opioid: Opioid medications increase the risk of sleep apnea.

Sleep apnea causes several minor inconveniences at the earlier stages. These symptoms are commonly ignored by the patients. People with sleep apnea do not get a peaceful sleep. They experience repeated awakenings throughout the night. These results in fatigue and their everyday activities are affected. The consequences of this fatigue include daytime drowsiness, lack of concentration and falling asleep in the middle of some work.

Also, since sleep apnea stops breathing, the sudden drops in blood oxygen levels may occur and this may lead to several cardiovascular problems [6].

Hilbert Huang Transform

To analyse the data which is nonlinear and non-stationary Hilbert Huang transform is used. This approach is unique and different from the existing methods. In this paper we use breathing sound as the input signal taken from the human body. The key part of the HHT is Empirical Mode Decomposition (EMD) and Hilbert Spectral Analysis (HSA) method. By EMD method, the target is decomposed in to a finite and small number of components, called as Intrinsic Mode Function (IMF), here the signal is decomposed in to time domain the length of the IMF is found to be same as that of original signal. Hilbert Spectral Analysis (HSA) is a method for examining the IMF’s instantaneous frequency and instantaneous amplitude as function of time [7].

Empirical mode decomposition (EMD)

The EMD is locally adaptive and suitable for analysing time series data representing nonlinear and non-stationary process. In this method any complicated data set can be decomposed in to a finite set of functions called ‘intrinsic Mode Functions’ (IMF’s). Instead of constant amplitude and frequency an IMF have variable amplitude and frequency along the time axis [8]. The procedure of extracting an IMF is called sifting. An IMF is defined as the function that satisfies two conditions:

1) In the whole data set, number of extrema and number of zero crossing should be equal or differ most by 1.

2) At any point the mean value of the envelope of local maxima and the envelope of local minima is zero.

The first step in applying HHT is to decompose the signal X (t) into IMF’s by using the EMD process. To find the IMF of the signal sifting process consist of following steps [7,9].

a) Identify all extrema (both maxima and minima) of X (t).

b) Create upper envelope U (t) and lower envelope L (t) by spline interpolation of local maxima and local minima respectively.

c) Calculate the mean for envelope, M (t)=(U (t)+L (t))/2.

d) The mean value of IMF should be zero, so subtract the mean signal M (t) from the input signal X (t).

H₁ (t)=X (t)-M (t)

e) The next step is to check the signal H₁ (t) is IMF or not.

f) If H₁ (t) is not an IMF then repeat the steps (a) to (e). Therefore in the second sifting process, H₁ (t) is treated as the data resulting in,

H₂ (t)=H₁ (t)-M (t)

Repeat this process n time, until we get the first IMF. Once the IMF is found it is defined as, C₁ (t)= H₁ (t). This is the finest temporal component in the time series data. After the IMF C (t) is found residue is defined as R (t), as the difference of this IMF and the input signal.

R₁ (t)=X (t)-C₁ (t)

To find all the IMF’s residue R₁ (t), is used as the input signal. The residue contains the information for the longer duration of time.

g) Test whether the residue is constant, a monotonic function or the maximum amplitude is below a threshold or a function with only maxima and minima, if so, terminate the EMD process, or else repeat step (a) to (f) and the result is,

R₁ (t)-C₂ (t)=R₂ (t)

R_n-1 (t)-C_n (t=R_n (t)

Stoppage criteria: 1) Standard deviation (SD): The sifting process stops when the difference between two consecutive sifting is smaller than the pre-given value.

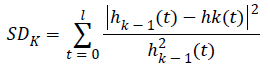
2) S Number criteria: the sifting process will stop only after S consecutive sifting; the number of zero crossing and extrema is equal or differ by 1.

3) Threshold method: Proposed by Rilling, Flandrin and Goncalves, threshold method set two threshold values to guaranteeing globally small fluctuations in the mean while taking in account locally large excursions [10].

EMD is completed when the residue does not contain any extrema points [11]. At the end of the decomposition the signal X (t), can be expressed as the sum of IMF’s and last residue.

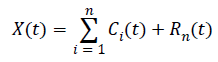
n-Number of IMF

R_n (t)-final residue

Hilbert spectral analysis (HSA)

The Hilbert transform is applied on each IMF and it is defined as,

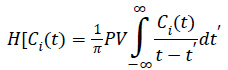
PV-Cauchy principle integral that is assigning value to certain improper integral which would otherwise be undefined. For any of the IMFs C_i (t), the corresponding i (t) is found by using Hilbert transform [12]. The analytical signal is given as,

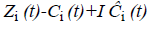
The magnitude of the analytical signal is the instantaneous magnitude,

A_i (t)=|Z_i (t)|

Instantaneous frequency is defined by using the instantaneous variation in phase angle,

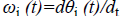
Where,

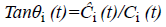
Where i=1, 2………….n

Once the Empirical Mode Decomposition (EMD) and Hilbert Spectral Analysis (HSA) is completed, the original signal is expressed as,

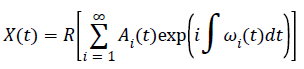
It is known that HHT is characterized by the sum of the finite number of adaptive base function.

Result and Discussion

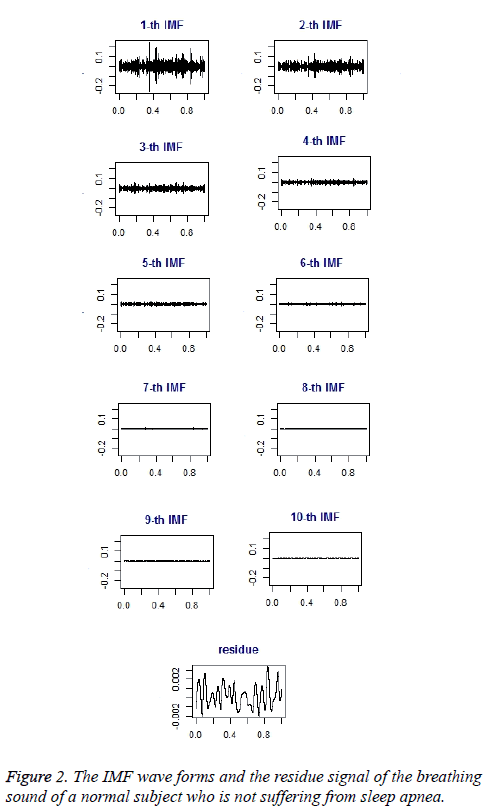
Figure 2 shows the IMF wave forms and the residual signal of the breathing sound of a subject who is not suffering from sleep apnea [13].

Figure 2: The IMF wave forms and the residue signal of the breathing sound of a normal subject who is not suffering from sleep apnea.

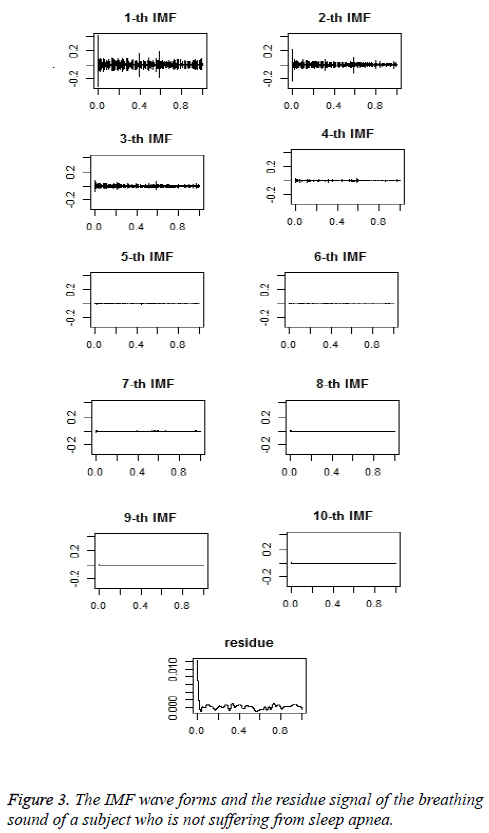
Figure 3 shows the IMF wave forms and the residual signal of the breathing sound of a subject who is suffering from sleep apnea.

Figure 3: The IMF wave forms and the residue signal of the breathing sound of a subject who is not suffering from sleep apnea.

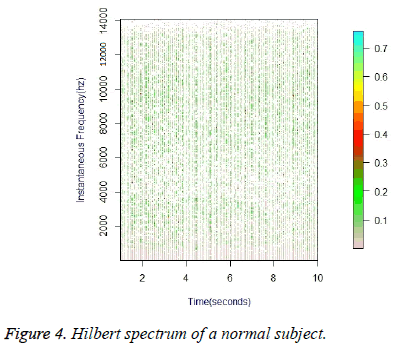
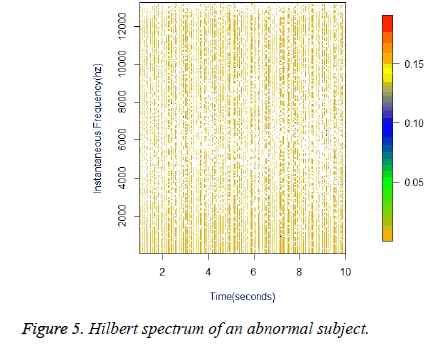
Figure 4 shows the Hilbert Spectrum of the breathing sound of a subject who is not suffering from Sleep Apnea while Figure 5 shows the Hilbert Spectrum of the breathing sound of a subject who is suffering from sleep apnea. As seen in the images, there is a clear difference between the spectrums of a healthy person as against the spectrum of a person suffering from sleep apnea.

Figure 4: Hilbert spectrum of a normal subject.

Figure 5: Hilbert spectrum of an abnormal subject.

Conclusion

In this study, a new method to predict the presence of obstructive sleep apnea is proposed. In this method, breath sound of the subject is recorded during wakefulness. The sound is then converted into signals and then Hilbert spectral analysis is performed. The Hilbert spectrum of the breathing sound of the people with OSA is shown to be tracing a pattern different from that of healthy people. In the Spectrogram of the healthy person, the amplitude is seen predominantly around 0.2, while in the Spectrogram of the person with sleep apnea, the amplitude is just about 0.01. As a result of this study, OSA can be detected by a simple, non-invasive and inexpensive method of screening and the process of detection is much quicker than conventional methods.

Acknowledgment

The authors wish to thank University Grants Commission (UGC) for providing funding for this research work.

References

1. Aman M, Zahra M. Acoustical screening for obstructive sleep apnea during wakefulness. IEEE EMBS Buenos Aires Argentina 2010.
2. de Silva S, Abeyratne UR, Hukins C. Impact of gender on snore-based obstructive sleep apnea screening. PhysiolMeas 2012; 33: 587-601.
3. Premkumar R, Arun C, SaiDivya R. Continuous wavelet analysis of the breathing sounds of obstructive sleep apnea patients and normal subjects during wakefulness. ApplMech Mater 2014; 622: 45-50.
4. Aman M, Zahra M. Obstructive sleep apnea prediction during wakefulness. IEEE EMBS Boston Massachusetts USA 2011.
5. Azadeh Y, Ali A, Aman M, Zahra M. Acoustical flow estimation in patients with obstructive sleep apnea during sleep. IEEE EMBS San Diego California USA 2012.
6. Azadeh Y, Frank R, Aman M, Douglas Bradley T. Variations in respiratory sounds in relation to fluid accumulation in the upper airways. IEEE EMBS Osaka Japan 2013.
7. Neha S, Mukesh T, Jaikaran S. Feature extraction of ECG signal using HHT algorithm. IJETT 2014; 8.
8. Paithane AN, Bormane DS. Electrocardiogram signal analysis using empirical mode decomposition and Hilbert spectrum ICPC, 2015.
9. Hassan S, Bruno J, Daniel E. EEG analysis using HHT: One step toward automatic drowsiness scoring. Adv Inform NetwAppl IEEE 2008.
10. Paithane AN, Bormane DS. Analysis of nonlinear and non-stationary signal to extract the features using Hilbert Huang transform. IEEE 2014.
11. Donghoh K, Hee SO. EMD: A package for empirical mode decomposition and Hilbert spectrum. Royal J 2009; 1.
12. Cong Z, Mohamed C. Hilbert-Huang transform based physiological signals analysis for emotion recognition. 4 Place Jussieu 75252 Paris Cedex 2005.
13. Peter V, Szabolcs B, Zoltan B. Detection of airway obstructions and sleep apnea by analyzing the phase relation of respiration movement signals. IEEE Trans InstrMeasur 2003; 52.