ISSN: 0970-938X (Print) | 0976-1683 (Electronic)
Biomedical Research
An International Journal of Medical Sciences
Research Article - Biomedical Research (2017) Artificial Intelligent Techniques for Bio Medical Signal Processing: Edition-I
Identification of hard exudates in retinal images
1Department of Electronics and Communication Engineering, Sathyabama University, India
2Department of Electronics and Communication Engineering, Veltech-Multi Tech Engineering College, India
- *Corresponding Author:
- Dhiravidachelvi E
Department of Electronics and Communication Engineering
Sathyabama University, India
Accepted on January 31, 2017
A new procedure for identification of the hard exudates is described in this Paper. Images are sorted into as many as 15 types using the maximum value of the hue in an image. Hue (h) at a point is defined as the ratio of green (g) to red (r) intensities. Given an image, the type-number is assigned to it. The exudates are also identified by using the hue, h. The varying intensities have been taken care of by the linear fit obeyed by the plot: h = m*g+c. A modified hue variable ‘Bh’ is used to eliminate the soft exudates which have a blue component, by fitting lines like Bh=w1*h+w2. Very low intensity yellow coloured patches which do not qualify as hard exudates are removed by a discriminating threshold ‘de’. The parameters like (m, c), (w1,w2), de are listed for the 15 types, in a Look up Table derived from experiments. The table entries vary in a structured manner. The tables can further be simplified as expressions if desired.
Keywords
Hard exudates, Soft exudates, Optic disc, Hue, Parameterization, Retinal image.
Introduction
Diabetic Retinopathy (DR), which is the major cause of blindness, could be slowed down by early detection. Automatic screening systems help in detecting the primary symptoms like exudates, which are due to the leakage of lipids from blood vessels. These have a peculiar yellow colour. Image processing methods for automated detection are largely based on thresholding on colour spaces.
Some pre-processing of the images is necessary, to take care of brightness and contrast variations. Colour normalization and contrast enhancement prior to the segmentation are discussed in [1]. Fisher’s linear discriminant analysis is one of the important tools for detecting retinal exudates [2]. The contrast of hard exudates is better in the green plane, in which intensity enhancement appears to be more successful. EM algorithm has been used for identifying hard exudates in [3]. Thresholds may be prescribed to perform the isolation of hard exudates from background and such procedures are usually very fast [4]. However the optimal threshold is not fixed for all the images, due to the variations in the histograms [5] of the different retinal images. Texture feature vectors, instantaneous amplitude and frequency etc., have also been used to identify structural similarities [6]. Hard exudates are characterized by bright sharp edged yellow regions of lipid deposits. Such exudates can be separated by fuzzy c-means algorithm [7]. Many procedures have been reported in the technical literature for the identification of the hard exudates. One major problem is due to the presence of the Optic Disc (OD) in the images.
The OD is whitish-yellow in colour. Elimination of the OD followed by fuzzy logic based hard exudate identification has been reported [8]. The precise segmentation of exudates by top hat-bottom hat morphological appears to provide effective support for laser treatment [9]. The various picture elements in an image appear to be associated with different clusters. However, a cluster with a unique property may not be physically seen as a single bunch [10]. Picture elements on a region contour, in contrast to the pixels at the interior regions of the contour may have grossly different membership values.
Dynamic thresholding had been considered in to optimize the thresholding process for identification [11]. Additional data like the age of the patient, gender and the type of diabetes have been given in [11], for the colour images analyzed by exudate-probability- map and wavelets. Increasing the brightness of the lesions near the fovea and general enhancement of the lesions and their extraction using DUCT had been considered in [12]. The proximity of the exudates to the optic disc implies that the severity of the disease is high. A hybrid approach consisting of pre-processing, clustering and post processing using morphological, Linde-Buzo-Gray and K means are discussed in [13]. Coarse and fine level histogram segmentation, reconstruction, and feature extraction had been discussed in [14] to identify the yellow exudates. Hard exudates appear as yellow spots or patches, with sharp margins in colour retinal images [14]. Even though the energy of hard exudates is more concentrated in the green region rather than the red region, the relatively brighter red intensities were also considered in [15]. The maximum intensity has been the guiding factor for lesion- identification in [16]. A multi-scale AM-FM decomposition of the retinal image and detection of lesions with a high degree of accuracy is found in [17]. A new method for normalizing images, de-ionizing and detecting reflections has been reported, which uses a random forest algorithm for identifying the exudates [18]. The edges and the shape had been considered by a method involving Markovian model [19].The exudates can be extracted using scale invariant feature transform. Non-linear background elimination leads to improved automatic detection of exudates [20]. The pixels outside the prescribed lower and upper bounds are rejected. Adaptation to varying brightness and contrast, cluster analysis by considering region contours and application of combinational mathematical morphology etc., have been discussed in [21]. Contrast adjustment transformation has been applied on green channel only, with the intensity enhanced in the darker regions [22]. Watershed transformation had been implemented for segmentation of exudates as a binary picture. For detecting the exudates, active contour model has been used, to achieve accurate boundaries for [23] the lesions. Haartransforms and other methods for exudate detection are found in [24,25].
The hard exudates on the retina are characterized by a peculiar yellow hue, which is different from that of the optic disc. Also the blue component in the hard exudates is either negligible or very small whereas in the case of soft exudates, the blue component would exist to an appreciable extent. This gives the soft exudates a whitish yellow colour. The optic disc may also appear whitish because of the blue component being liberally present. If the blue component had been filtered out in the given image, the colour of the optic disc as well as the soft exudates will compete with the hard exudates, making the latter’s separation very difficult. The retinal images are taken under different lighting conditions. Even if the same instrument (ophthalmoscope) had been used under controlled lighting conditions, the images would be different for different patients. In this Paper, the identification of the hard exudates alone would be discussed. The identification of the Optic disc location was discussed in [26]. With the center and the radius of the optic disc (OD) known, the image can be blotted out in this region. Any falsely identified ‘hard exudate’ within the OD region would be blanked out.
The soft exudate can be removed by examining the blue tinge. After eliminating these competing factors, in the very large left over region on the retina, the exudates are to be located. The problem can now be stated: “Can the characteristic yellow colour of the hard exudate be parameterized so that it could be isolated using Mathematical Logic, and hence a Program?” An interesting line-fitting technique is being described in this Paper, which helps to locate almost all the points where the hard exudates may exist. It may be noted that rather than ‘regions’, ‘points’ are being identified in this work. The Program has been written as an m-file, which is very short and takes very little time to execute in a PC.
HUE, RGB Normalization of the Retinal Images
Hue equalization of the central bulk
The supplied images may exhibit different brightness and Hues. The images are normalized so that the resulting image presents the same bulk-average (gross-average) hue. The hue at a point itself is simply defined as the ratio of the green value to the red value of the pixel under discussion. The spatial average of the hue, (excluding the corners which are black) of a given image is to be normalized. The procedure had been explained in the earlier Paper [26].
Let the given Image be: [Xr (i,j), Xg(i,j), Xb(i,j)]
Hue matrix be: [H(i,j) ]=[ Xg (i,j)/Xr (i,j)],
for Xr (i,j) >rT>0 (1)
In the above, rT, the threshold for Xr(i,j) is a small positive number (say=0.1) to avoid division by zero.
Let the desired bulk-average hue of the image be hdes (say=0.5160). This is the average hue of a base retinal picture ‘image005’, available in the reference [27].
By a process of iteration which involves simultaneous point by point adjustment of the R-intensity and green intensity by ‘Δ’, the bulk-average Hue can be changed [26]. The changed hue matrix is:
[ Hc(i,j)]=[(Xg(i,j)+Δ)/Xr(i,j)-Δ)]. (2)
The average of [Hc] namely hc_ave is compared with the desired hdes and Δ is adjusted so that hc_ave=hdes. The above process can be done only iteratively. It however converges within about 3or 4 recursions.
RGB normalization
After Hue normalization, the gross average of R, G, B components are individually computed.
Let these be: Rav, Gav, Bav.
Let the desired averages be Cr, Cg, Cb.
Cr=120, Cg=40 and Cb=15 were assumes to be fixed for all program used
RGB Normalization is an easy single step linear process.
Xr=Xr–Rav.I+Cr.I
Xg=Xg–Gav.I+Cg.I
Xb=Xb–Bav.I+Cb.I (3)
Definition: hue and discrimination
At any point, the hue is defined as:
h(i,j) = Xg (i,j)/Xr (i,j) (4)
The hue for the exudates may be defined as:
he(i,j) = Xg(i,j)/Xr (i,j) (5)
Another discriminating factor de(i,j) has been defined to include the exudates and exclude some yellow colored points which are not exudates but probably, fragments of the optic disc or soft exudates.
de (i,j) =[Xr(i,j)-Xg(i,j) ]/Xg(i,j)
Experimentation on the Hard Exudates
The reason for gross-Hue normalizing is that, the hue is the parameter chosen in this paper, by which the hard exudates are proposed to be identified. After gross-Hue normalization and RGB bulk-average normalization, experimentation could be carried out in the given retinal image samples.
Linearization
To begin with, an image known to contain hard exudates is taken. The RGB values at the various points where the hard exudates are located are noted down. About 30 to 40 readings may be extracted in this manner. The hue he (i,j) is plotted against the green signal, Xg (i,j). Similarly, de (i,j) is plotted w.r.t. Xg (i,j).
In many cases a linear fit would be sufficient. If the images were very bright, then the exudate would show large Xg; then saturation is seen and hence a quadratic fit may be necessary for more accurate parameterization. After normalization with the above numerical parameter values, the linear fit is more often seen in the various images than the quadratic fit.
Similarly, the region inside the OD is whitish yellow in colour and can be analyzed by defining: ho (i,j) and do (i,j). The plots of ho (i,j) and do (i,j) w.r.t Xg (i,j) are also reasonably linear.
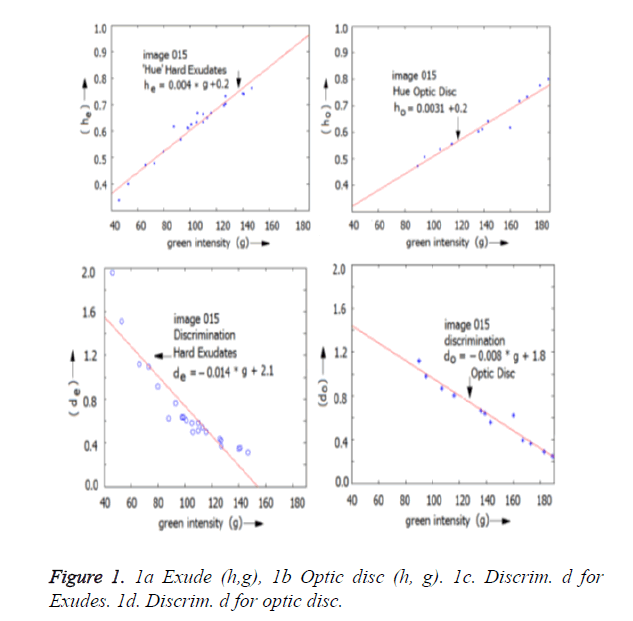
For example, for an image termed ’image015’,
he=0.004*Xg+0.2; (7)
de=-0.014*Xg+2.1;
The line-parameters for the exudates are;
(me, ce)=(0.004, 0.2)
(pe,qe)=(-0.014, 2.1)
Further, for the optic disc of the same picture image 015:
ho=0.0031*Xg+0.2
do=-0.008*Xg+1.8 (8)
The line-parameters for the OD are:
(mo, co)=(0.0031, 0.2)
(po, qo)=(-0.008, 1.8)
The various lines are shown in Figures 1a-1d. In general, the h-line for the exudates is above that of the h-line of the optic disc. The d-line for the exudates is in mostly located lower than that of the optic disc.
Since a complete or fully satisfactory hue and RGB normalization is not possible, the parameters (me k, ce k) for the images k=1,2,---,30, may not be identical; however, these may be very close to each other.
Generally, the various normalized images showed m 0.004 and 0.20<ce<0.24. In some extreme cases like a very dim picture, c may be as low as 0.14. Similar arguments hold good for (pe k, qe k). A hard exudate in the image ‘k’ would satisfy both (me k, ce k) and (pe k, qe k).
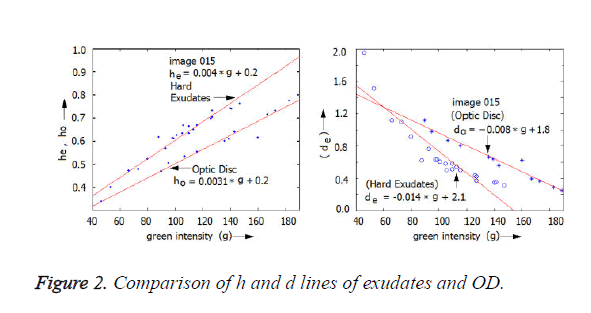
In Figure 2, the lines of the exudates as well as the optic disc were superimposed. The separation gives an assurance that these parameters can indeed be used to isolate the exudates from the optic disc.
Sorting the images into types
It also appears that the parameters (me k,ce k), (mo k,co k) etc., may bear a relationship with some other derived parameter of the picture-k. In other words, there should be another parameter that would be useful for sorting and clubbing together the images which may have similar values for mk and ck.
Before normalization procedure, exhaustive experimentation had been carried out on various images. Statistical parameters like Rmax, Gmax, Bmax, Rave, Gave, Bave, hmax, have and many others were determined for the central bulk portion of the retinal image. It was found that hmax was a reasonably dependable parameter for sorting purposes. The maximum value of the hue found within the circular retina, excluding the optic disc, is defined to be hmax.
In fact the type number has been assigned not just based on the discrete values for hmax but for a range of ‘maximum h’. This is shown in Table 1.
| Type (k) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| hmax | 0.45 | 0.53 | 0.56 | 0.59 | 0.61 | 0.62 | 0.64 | 0.66 | 0.69 | 0.71 | 0.74 | 0.79 | 0.84 | 0.88 | 0.95 |
| Range of hmax |
0.40 to 0.50 |
0.50 to 0.55 |
0.55 to .575 |
.575 to .605 |
.605 to .620 |
.620 to .625 |
.625 to 650 |
.650 to .675 |
.675 to .700 |
.700 to .725 |
.725 to .750 |
.750 to .825 |
.825 to .855 |
.855 to .900 |
.900 to 1.00 |
Table 1. Range of hmax and type_number of images.
Parameter tabulation for identification
With the sorting parameter as hmax, hue-line parameters of the exudates, viz., (me k, ce k), have been shown in Table 2. In the same table, the maximum value of de k have also been entered. The images have been arranged in the descending order of hmax. These are the main parameters used for identification.
| Type (k) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| hmax | 0.45 | 0.53 | 0.56 | 0.59 | 0.61 | 0.62 | 0.64 | 0.66 | 0.69 | 0.71 | 0.74 | 0.79 | 0.84 | 0.88 | 0.95 |
| mek | m= 0.0040 (approximately constant) | ||||||||||||||
| cek | 0.14 | 0.23 | 0.23 | 0.23 | 0.24 | 0.24 | 0.22 | 0.22 | 0.22 | 0.22 | 0.22 | 0.22 | 0.22 | 0.22 | 0.22 |
| dmaxk | 1.55 | 1.35 | 1.35 | 1.35 | 1.35 | 1.35 | 1.35 | 1.35 | 1.25 | 1.2 | 1.1 | 1.1 | 1.05 | 1.02 | 1 |
Table 2. Variation of Hue_ Line Parameters with hmax.
To verify whether a point (i,j) in the image-k is a hard exudate or not, we calculate he k=Xg(i,j)/Xr(i,j);
We also estimate: h. me k.g+ck
and compute he k=g/r
de k=(r-g)/r
where: g=Xg(i,j) and r=Xr(i,j); (9)
(i) If |ĥ-hek|<0.15.hek
and de k<demax k, (10)
then the point (i,j) is a good candidate for Hard exudate.
It may contain noisy patches which may be removed by thresholding. The thresholds are also functions of hmax.
(ii) If he k>hL k (Lower bound) (11)
then, the point is accepted as a hard exudate.
This threshold has been determined experimentally and the factor FC has been tabulated for various hmax, such that:
hL k=hmax/Fc.
(iii) Additionally, he k>hoptic
where, hoptic is the average intensity of the optic disc. This is effective for removing the stray-noise near the optic disc.
Elimination of soft exudates
With the above three constraints applied, the exudates may be easily isolated. However, it may be a mixture of hard and soft exudates. The latter may have a whiter tinge than that of the hard exudates. In other words, the hard exudates would show a very small blue component, in the RGB normalized image (say<15). However, a large blue component (say>55) indicates soft exudates. Hence, one more rule is to be introduced to exclude the softer exudates, which have blue components.
Experimentation had been carried out, with the help of known results for eliminating soft exudates [27].
A new variable Bhk has been introduced, which is similar to hk, but the blue component is also considered in the expression.
Bh=(g-b+15)/(r-b+15) (14)
In the above variable, the Blue component has been essentially removed in computing the Hue.
(iv) If (L1 k<Bh k<L2 k), then it is a not a hard exudate.
where, L1 k=wM k*h+wC1 k
L2 k = wM k*h + wC2 k
Another thresholding rule, essentially to overcome the noise can be formulated. A parameter Bf k is introduced. It is built out of the averages in the local 5 × 5 region.
(v) (bav/gav) <Bf k; (16)
The ratio of blue average to green average should be less than Bf. The various thresholding parameters obtained experimentally are shown in Table 3. These LUT’s can be used as such. These can also be used to generate fuzzy logic rules if necessary.
| Type (k) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| hmax | 0.45 | 0.53 | 0.56 | 0.59 | 0.61 | 0.62 | 0.64 | 0.66 | 0.69 | 0.71 | 0.74 | 0.79 | 0.84 | 0.88 | 0.95 |
| Fc | 1.1 | 1.2 | 1.3 | 1.33 | 1.4 | 0.41 | 1.45 | 1.5 | 1.55 | 1.55 | 1.55 | 1.55 | 1.65 | 1.85 | 1.95 |
| Bf | 0.37 | 0.37 | 0.37 | 0.37 | 0.39 | 0.39 | 0.4 | 0.4 | 0.4 | 0.4 | 0.4 | 0.4 | 0.42 | 0.42 | 0.42 |
| WM | 0.78 | 0.78 | 0.8 | 0.8 | 0.8 | 0.8 | 0.8 | 0.8 | 0.85 | 0.85 | 0.86 | 0.86 | 0.86 | 0.87 | 0.87 |
| WC1 | 0.02 | 0.02 | 0.03 | 0.03 | 0.02 | 0.02 | 0.02 | 0.02 | 0.015 | 0.015 | 0.01 | 0.01 | 0.01 | 0.02 | 0.02 |
| WC2 | 0.06 | 0.06 | 0.063 | 0.063 | 0.03 | 0.03 | 0.03 | 0.03 | 0.05 | 0.05 | 0.04 | 0.04 | 0.04 | 0.035 | 0.035 |
Table 3. Parameters for elimination of whitish exudates and noise.
Summary for hard exudate identification
1. The maximum hue (g/r) is found out in the region excluding the optic disc. Accordingly a type_no. is given to the image.
2. The bulk of the given image ‘k’is hue-normalized to h = 0.5190 (ref image is image005)
3. The bulk average RGB brightness are normalized to (120,40,15)
4. Using the type number, (mek,cek) and dmaxk are extracted from Table 2.
5. At every point (i,j) in the image the hue h=g/r is computed. It is checked whether the pair r=Xr (i,j) and g=Xg (i,j) satisfy: he (i,j)=me k.g+ce k; (parameters mek, cek are from the table).
6. If the inequality: |he–h|<0.15* he; with h=g/r is satisfied, then it is good candidate for an exudate.
7. The noise in bulk region is eliminated by using thresholds for ‘h’ (=hmax/Fc); (parameter Fc is from the table).
8. Near the optic disc, noise is eliminated using the threshold for ‘h’ (= hoptic_ave); (from program)
9. Soft or whitish exudates are removed by using parameters wM, wc1, wc2.
Bh k=(g-b+15)/(r-b+15); ( L1 k<Bh k< L2 k), then it is a not a hard exudate.
where, L1 k=wM k*h+ wC1 k
L2k=wM k*h+ wC2 k;
(the parameters, wM k, wC1 k wC2 k are from the table).
10. Also, (bav/gav) <Bf k; the ratio of blue average to green average should be less than Bf for hard exudate. (Bf is from the table). The local averages are computed in a (5 × 5) neighbourhood.
11. Further, reflections from smooth retinal surfaces are eliminated using (5 × 5) texture filters like:
(σR/Rav)>0.037 ∩ (σ H/hav)>0.05 ∩ (σD/dav)>0.06 where, Rav hav, dav are the local averages of R, hue and d. σR, σH, σD are the corresponding standard deviations of R, hue ‘h’ and the discriminating factor ‘d’.
12. Successfully identified hard exudates are stored in a separate BW matrix Y(i,j) as entries 255.
13. A few pieces of the optic disc may have been falsely identified as hard exudates (optic disc-noise). Hence, the optic-disc- region needs to be blotted out adaptively. This is done by moving a circular blanking filter left or right, up or down, one pixel at a time, checking whether the total count of white (255) pixels is the least in the BW image Y. The maximum movement of the mask, in any direction has been limited to 4 pixels. This procedure also helps to overcome the error in the location of the optic disc which contributes a crescent like segment being falsely confirmed as a hard exudate. In short, using the optic disc identification techniques [26], the location (center) is determined. The radius of the optic disc for the 197 × 256 size pictures is 21 to 22 pixels.
Examples and Results
Examples for hard exudates
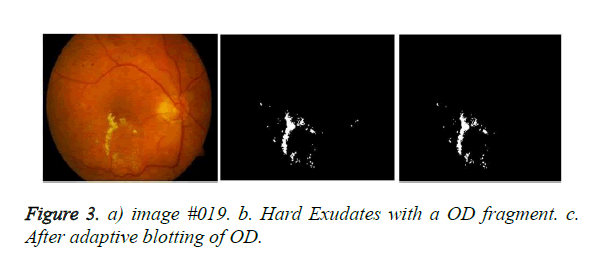
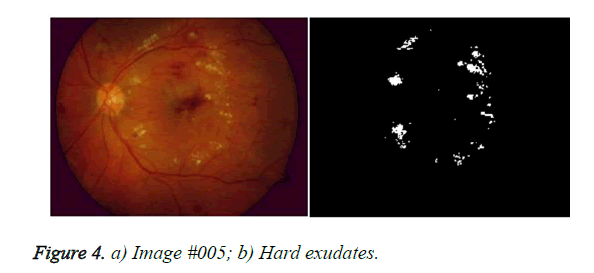
In Figure 3, a severe case of hard exudates is seen. The OD is smudged and the periphery is not very clear. The hue and RGB normalized of the image #019 [27] is shown in Figures 3a. The picture size is 256 × 197 × 3. In the original Image, the blue component is absent; probably, it had been filtered out. The identified hard exudates are shown in Figure 3b. The optic disc and the exudates are yellow in colour. However, there is a difference in hue. Excepting for a small piece of the optic disc, the most of the optic disc had been either identified ‘not as exudates’ or had been blotted out. In Figure 4a, the optic disc boundaries of the image #005 are well defined. This image contains hard and soft exudates. The blue component is liberally present in many regions. Most of the soft exudates have been successfully filtered out, leaving behind the hard exudates. In Figure 4b, shows the detected hard exudates. It is probable that some hard exudates have vanished along with the soft exudates.
Tabulation of results
Using the data provided by the experts (Figures 5a and 5b) the percentage of points correctly classified as hard exudates in the BW matrix Y had been computed for the above two images. The expert results appear to be largely conservative so that larger regions are marked to be affected by hard exudates. Tests were performed at least on 30 images [27] in which the hard exudates alone existed. The success rate for the various test images is shown in Table 4.
Figure 5. a) Expert Result [27] for image #019; b) Expert Result [27] for image #005.
| Im_ID # | 001 | 002 | 004 | 005 | 006 | 007 | 008 | 010 | 011 | 012 | 013 | 014 | 015 | 016 | 017 | 018 |
| Type No: | 9 | 1 | 7 | 12 | 6 | 4 | 4 | 2 | 7 | 10 | 5 | 14 | 13 | 9 | 4 | 10 |
| Success%: | 100 | 40 | 100 | 95.3 | 100 | 100 | 100 | 100 | 90.5 | 100 | 100 | 100 | 99.2 | 99.1 | 75.0 | 100 |
| Im_ID # | 019 | 020 | 021 | 022 | 023 | 024 | 025 | 027 | 035 | 038 | 052 | 053 | 066 | 067 | 084 | 085 |
| Type No: | 15 | 10 | 6 | 5 | 2 | 7 | 11 | 2 | 2 | 2 | 1 | 5 | 3 | 9 | 11 | 8 |
| Success%: | 99.8 | 35.9 | 100 | 100 | 100 | 99.4 | 98.5 | 0 | 100 | 100 | 0 | 100 | 100 | 100 | 95.7 | 0 |
Table 4. Success rates of identification of hard exudates in images.
Comments on successful images
It is seen that from type-2 to type 15, the success rates were similar. Probably, the hmax does not have much influence on the success rate. An exception is very dim images. Further, type_8 to type_12 images have consistent parameter values. If the retinal image is made to fall into these types, then identification of the exudates can be can be made faster. In such a case even the LUT may become redundant.
Comments on failed images
Image #017: success rate is 75%. There are very few spots. Out of these, one small spot identified by the program as ‘hard’ is ‘soft’ according to the expert.
Image #002: success rate=40%. The automatic threshold setting of this dull-type-2 image is very difficult.
Image #020: Success rate=35%.The image is bright enough (type 12); however, there are more soft exudates than hard exudates. Some of the exudate regions with small blue component have been assigned as ‘hard’ by the program. However, the expert has assigned them to the ‘soft’ type.
Image #27: Success rate=0%. The image is very dull (type 2). Setting the threshold automatically is very difficult.
Image #52: Success rate=0%. The image is very dull (type 2); setting the threshold automatically is very difficult.
Image #85: success rate=0%. Even though the image is bright enough (type 8), most of the illumination had been directed on to the optic disc. The exudates themselves are in the poorly illuminated region.
Conclusions
It has been shown that the given retinal images can be sorted into about 15 types based on the maximum yellow-hue in the non-optical region of the retina. The exudates and the optic disc of the retinal images can be parameterized and numerical values fixed so that automatic identification and separation via a computer program is made more meaningful. Similar parameters of the straight line fit can be used to preclude soft exudates and fragments of the optic disc, which have a fairly large blue component. These parameters, for a variety of images, are reasonably close to each other because of the hue normalization and RGB normalization done on the given retinal images. The tabulated parameters can be converted into piecewise linear expressions if required. The table also helps in developing a fuzzy logic based classifier. The OD may not be truly circular small variations are possible for different patients. In spite of the separation between the OD and the exudates, there is a possibility of small segments leaking from the OD and appearing falsely as exudates, particularly near the periphery of the OD. Such cases can be taken care of by adaptively introducing small changes in the center and the radius of the OD while blotting out the OD region. This also corrects the location errors of the Optic Disc. Another interesting bye product of the Table is that, in the middle region, representing a few types, the parameters are reasonably constant. Hence, even while taking the retinal pictures, if the average bulk image intensities, hue etc., are made similar, automatic identification may yield better results.
References
- Sareh A, Shadgar B, Markham R. Computational-intelligent-based approach for detection of exudates in diabetic retinopathy images. IEEE Trans Inf Technol Biomed 13; 2009.
- Sanchez CI, Hornero R, Lopez MI, Aboy M, Poza J, Abasolo D. A novel automatic image processing algorithm for detection of hard exudates based on retinal image analysis. Med Eng Phys 2008; 350-357.
- Sanchez CI, Garcia M, Mayo M, Lopez MI, Hornero R. Retinal Image analysis based on mixture models to detect hard exudates. Med Imag Anal 2009; 650-668.
- Akarasopharak A, Uyyanonvara B, Barman S, Williamson TH. Automatic detection of diabetic retinopathy exudates from non-dilated retinal images using mathematical morphology methods. Comput Med Imaging Graph 2008; 32: 720-727.
- Sanchez CI, Garcia M, Mayo A, Lopez MI, Hornero R. Retinal Image analysis based on mixture models to detect hard exudates Med Imag Anal 2009; 650-668.
- Agurto C, Murrary V, Yu H, Wigdahl J, Pattichis M, Nemeth S, Barriga ES, Soliz P. A Multi-scale AM-FM Methods for Diabetic retinopathy Lesion Detection. IEEE Trans Med Imaging 2010; 29: 1-16.
- Singh N, Tripathi RC. Automated Early Detection of diabetic Retinopathy using Image Analysis Techniques. Int J Comput Appl 2010; 8.
- Ranamuka NG, Gayan R, Meegama N. Detection of hard exudates from diabetic retinopathy images using fuzzy logic. IET Image Process 2012.
- Ghafourian M, Eadgahi F, Reza H, Reza P. Localization of hard exudates in retinal fundus image by mathematical morphology operations. J Theoret Phys and Cryptograp 2012; 1.
- Ravindraiah R, MazharIqbal JL. Hard exudates detection in proliferative diabetic retinopathy using gradient controlled fuzzy c means clustering algorithm. GESJ 2014; 44: 4.
- Giancardo L, Meriaudeau F, Karnowski TP, Li Y, Garg S, Tobin KW Jr, Chaum E. Exudate based diabetic macular edema detection in fundus images using publicly available data sets. Med Image Anal 2012; 16: 216-226.
- Esmaeili M, Rabbani H, Dehnavi AM, Dehghani A. Automatic detection of exudates and optic disk in retinal images using curvelet transform. IET Image Process 2011.
- Kekre HB, Sarode TK, Parkar T. Hybrid approach for detection of hard exudates. Int J of Advanc Comp Sci Appl 2013; 4.
- Bu w, Wu X, Chen X, Dai B, Zheng Y. Hierarchical detection of hard exudates in color retinal images. J Soft 2013; 8: 11.
- Sreng S, Maneerat N, Isarakorn D, Pasaya B, Takada J, Panjaphongse R, Varakulsiripunth R. Automatic exudate extraction for early detection of diabetic retinopathy. IEEE 2013.
- Nidhal K, Abbadi E, Hamood Al-saadi E. Automatic detection of exudates in retinal images. Int J Comp Sci 2013; 10: 1.
- Agurto C, Murrary V, Yu H, Wigdahl J, Pattichis P, Nemeth S, Barriga S, Soliz P. A Multi-scale optimization approach to detect exudates in the macula. J Biomed Heal Infor 2014; 18: 4.
- Zhang X, Thibault G, Deceniere E, Marcotegui B, Danno R, Cazuguel G, Quellec G, Lamard M, Massin P, Chabouis A, Victor Z, Erginary A. Exudate detection in color retinal images for mass screening of diabetic retinopathy. Med Ima Anal 2014; 18: 1026-1043.
- Harangi B, Hindu A. Detection of exudates in fundus images using a markovian segmentation model. IEEE 2014; 130-133.
- Akter M, Rahman A, KamrulIslam AKM. An Improved method of automatic exudates detection in retinal images. Int J Innov Res Elect, Electron, Instrument Cont Engin 2014; 2.
- Amel F. Mohammed M, Hafid BA. Improvement of the hard exudates detection method used for computer-aided diagnosis of diabetic retinopathy. Int J of Imag, Graph Sign Process 2012; 4: 19-27.
- Sowmya K. A novel algorithm for exudates detection using matlab, Intern J Advan Res Comp Sci Soft Eng 2015; 5.
- Bhargavi R, Rajesh V. Exudate detection and feature extraction using active contour model and sift in color fundus images. ARPN J Eng Appl Sci 2015; 10.
- Rokade PM. Automatic hard exudates detection from multi-resolution retinal images using haar duel tree wavelet transform. Int J Comp Sci Tren Technol 2015; 3.
- Gaikwad NN, Pravinkumar R. Image processing technique for hard exudates detection for diagnosis of diabetic retinopathy. Int J Rec Innov Tren in Comput and Commun 2015; 3.
- Dhiravidachelvi E, Rajamani V, Janakiraman PA. Speedy location of the optic disc in retinal images. J Med Imaging Health Inform 2016; 6: 1906-1912.
- Kauppi T. Diaretb1, Diabetic retinopathy data base and evaluation protocol.