ISSN: 0970-938X (Print) | 0976-1683 (Electronic)
Biomedical Research
An International Journal of Medical Sciences
Research Article - Biomedical Research (2017) Volume 28, Issue 22
Lifetime maximization in wireless body area sensor networks
Mehdi Effatparvar1, Mehdi Dehghan2* and Amir Masoud Rahmani1
1Department of Computer Engineering, Science and Research Branch, Islamic Azad University, Tehran, Iran
2Computer Engineering Department, Amirkabir University of Technology, Tehran, Iran
- *Corresponding Author:
- Mehdi Dehghan
Computer Engineering Department
Amirkabir University of Technology, Iran
Accepted date: October 11, 2017
Wireless body area sensor network is a special-purpose wireless network that, employing wireless sensor nodes, is located within the human body area and transmits his vital signs. A node, placed on or near the human body, functions as the sink to collect data and finally transmit the captured data toward the central station. Here, we assume that sensors are fixed on the patient’s body, all sensors are capable of sensing and transmitting solely a certain type of vital signs data, all sensors serve both as routers and as data-generating sources, and there is no particular node serving as a relay. Network lifetime and energy consumption have significant role in WBASNs. In this paper we present a mixed-integer programming problem to balance energy consumption and maximize network lifetime. We introduce this model based on the initial energy, the energy received and transmitted by sensors, the rank or significance of sensors, the reliability of sensors, current temperature of sensors, and link bandwidth. The proposed method not only maximizes the network lifetime, but also considers many factors to find the next hops for each sensor. We used the General Algebraic Modeling System (GAMS) software to analyse results, find the routes from each sensor to the sink, and subsequently demonstrate the applicability of the proposed model. Moreover, the network lifetime in different cases of this method is evaluated and compared with that in other methods. Obtained results show a significant improvement in the network lifetime as well as greater durability of important sensors.
Keywords
Wireless body area sensor networks, Lifetime, Routing, Reliability, Initial energy, Energy consumption, Rank of sensor
Introduction
Wireless body area sensor network is a special-purpose wireless sensor network that, employing wireless sensor nodes in, on, or around the human body, makes it possible to measure biological parameters of a person, allows for remote health monitoring, and comes in wearable and implantable forms. These systems make substantial contributions to individuals by providing services such as medical monitoring, medical and pharmaceutical information provision, memory enhancement, control of home appliances, and emergency communication [1,2]. The concept of body area network was first proposed by Zimmerman in 1996 [3], and this technology was standardized by IEEE 802.15.6. Since the sensors used in wireless body area networks provide users with more convenience, this type of body area network is more widely used compared to wired body area networks, and can be implanted or worn [1]. There is a base station in these networks which receives collected information by sensor nodes and sends it to distant centers. This is one of the latest technologies in the field of diagnosis and health care management. The reason why it is important to use wireless body area sensor networks in medical environments is that these networks offer patients the unique opportunity to receive medical care at their homes instead of hospital environments, thereby playing a significant role in their health status.
Since it is costly and complicated to implant sensors in the human body, maximizing body area network lifetime and controlling sensor energy consumption are among major challenges in this regard [4,5]; on the other hand, precise and accurate information transmission in these networks seems to be highly important and challenging [6,7].
Other factors such as delay, security, or sensor temperature can be considered in a general concept of reliability in information transmission, and they can be used for transmitting vital signs of the patient’s body along with energy consumption control. Some of the existing restrictions in WBASNs-including realtime transmission of vital signs data control of sensor temperature during data transmission, and data transmission security-have caused energy consumption control and network lifetime maximization in these networks to be different from those in wireless sensor networks.
Since a person may have multiple diseases and various sensors might have been implanted in his body to sense his vital signs and relay them to a destination, the durability and stability of some of these sensors are more important than those of other sensors [8,9]. In other words, the priority of sensors varies depending on the person’s type of disease, and therefore, it is of more importance to control the energy consumption of highpriority sensors. Since direct data transmission toward the sink consumes a lot of energy and is not recommended but for critical data, multi-hop data transmission is generally used for data transfer operations [10,11]. In this type of transmission, however, intermediate nodes are involved in receiving and forwarding data, thereby consuming more energy. Now, if important sensors in multi-hop data transmission play the role of intermediate nodes and become involved in transmitting the information of other sensors, then the energy consumption of these sensors increases and their lifetime decreases [12]. Relay nodes have been used as intermediate nodes and error recovery approaches presented in some of the proposed methods [13-15], giving rise to challenges such as positioning of relay nodes, management of data transmission toward the relay, and also an increase in costs. Besides, sensor temperature increases by each transmission and the followed path may not be of use for the next transmission. Thus, the dynamics of temperature and energy levels of sensors are among major factors in multihop routing. Several studies, e.g. [16-19] have discussed control of sensor temperature, but the considerable point is that other important factors in data transmission have not been taken into consideration in the majority of these studies.
As we know many papers have already been proposed about the lifetime maximization in sensors network [9,12,20,21] but the in wireless body area sensor networks the some parameters are different and we have more constrains. Some of the presented methods save the energy by cross layer designing [22] and the others can save it by designing energy efficient topology and MAC protocols [23,24]. In [25] a relay selection scheme is proposed under the topology constrains specified in the IEEE 802.15.6 standard to maximize the lifetime of WBANs through formulating and solving an optimization problem but neither this paper nor the other previous works in wireless body area sensor networks have not considered multi parameters in their models to maximize the lifetime of WBANs. Usually previous works have proposed their algorithms without any mathematical proof and evaluations. In this study, we present a model for lifetime maximization in wireless body area sensor networks. In fact, the proposed model maximizes the time before the death of the first sensor node in the network and therefore increases stability of the whole network. This goal is achieved by taking into consideration restrictions such as energy level, reliability, bandwidth, and priority of sensors. The proposed scheme not only regards to maximize the lifetime, but also considers many factors to find the next hop for each sensor.
As we know Star and Multi-hop methods are important topology in body area networks. Results yielded by the proposed model are compared with those produced by Star and Double-hop methods.
The present paper is organized as follows. The proposed model is introduced and fully explained in section 2. Section 3 deals with solving the model and result analysis. Finally, conclusion and future works are presented in section 4.
Lifetime Maximization in WBASNs
In this section, we aim to achieve maximum lifetime for wireless body area sensor networks by considering limitations associated with the network. To this end, the energy of sensor nodes needs to be utilized in a balanced way; that is to say, all sensors in the network are required to transmit and relay data toward the sink in a balanced way in order that the death of the first sensor in the network occurs later, leading to increased network lifetime. In addition to fulfilling the operational task of analyzing human body’s vital data, a sensor node must forward the received information from other sensors toward the sink. It is obvious that both of these operations consume energy. Hence, it is necessary that a balance should be found between data transmissions of different sensors that much more than merely one or a few sensors should be involved in the data transfer operation. For better understanding we develop and describe our model step by step and finally we propose model [12] and we describe it completely.
For any i, let Ei be the initial energy of the ith sensor. Besides, assume that eijT denotes the amount of transmitted energy from sensor i to sensor j, and ejiR represents the amount of received energy by sensor j when transmitted by sensor i. Moreover, suppose xij k denotes the flow transmitted from sensor i to sensor j while the information belongs to the kth sensor. Thus, the total energy consumption of the ith sensor is calculated by
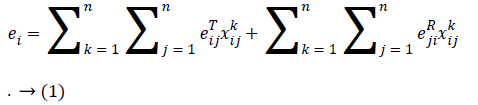
The lifetime of the ith sensor is obtained by dividing its initial energy (Ei) by its energy consumption; that is,
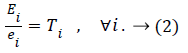
Since the network lifetime ends as soon as the first sensor node fails, it can be defined as follows:
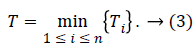
Let (i k) bik be the transmission rate of sensor i when the information of sensor k is transferred, then
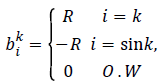
with R being the transmission rate of sensor i with respect to the information of sensor k. If bik=-R, then sensor i is the information transmitter. If i is equal to the sink, then bik=-R because the sink is the information receiver; and when it is an intermediate sensor, bik=0. Furthermore, assume each sensor i has capacity ui. In fact, ui is the total input information to sensor i. Thus, we propose the following model for maximizing the network lifetime, whereby at least one path is obtained for each sensor:
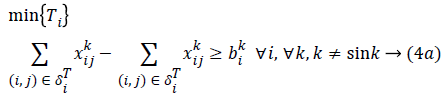
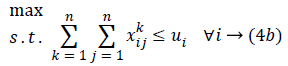
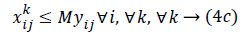
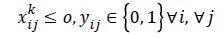
The objective function in Equation 4 is a max (min) function, which is non-linear. Changing variables, we can convert it into a linear form. Suppose
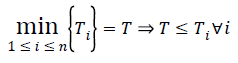
and since Ti=Ei/ei, then
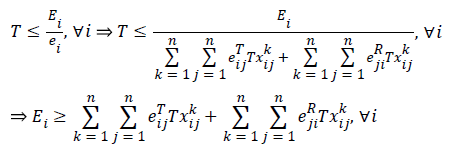
Considering the fact that 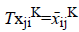 (since T ≥ 0, then ͞xij K ≥ 0), the above relation can be rewritten as follows:
(since T ≥ 0, then ͞xij K ≥ 0), the above relation can be rewritten as follows:
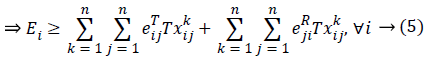
Constraints 4a express that the difference between the output flow from sensor i and the input flow to sensor i should be at least equal to the transmission rate of sensor i for the information of sensor k; if the constraints hold with equality, the flow rule is achieved. It should be noted that the available neighborhood for sensor i is denoted by δjT, and Constraints 4a are written for those sensors between which there exist routes.
In fact, Constraints 4a can be written as the following three categories of constraints:
a). If i equals the sink, then the sum total of transmitted information by sensor j that reaches the sink must be at least equal to the sink’s transmission rate for the information belonging to sensor k; that is to say,
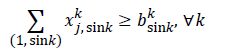
b). If i is the sensor generating information related to sensor k, then
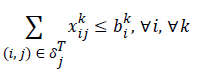
c). where only one type of data is transmitted. If more than one sensor generates information, then
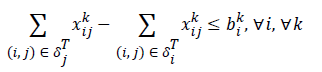
d). If i is the intermediate sensor, then
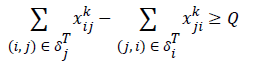
Constraints 4a show that the total aggregate flow from sensor i to sensor j for the information related to the kth sensor cannot exceed the capacity of sensor i. Since (i, j) yij is a binary variable, Constraints 4c declare whether or not there exists any path from sensor i to sensor j. If yij=1, then Constraints 4c change as xijk ≤ M; and since M is an extremely large positive number, it can be deduced that there is a flow, and therefore a path, from sensor i to sensor j. On the other hand, if yij=0, then constraints 4c change as xijk ≤ 0; and since xijk≥ 0, it can be concluded that xijk=0, implying there is no path from sensor i to sensor j. Hence, we propose the following linear model for the network lifetime maximization:
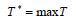
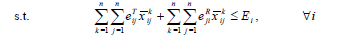 (6a)
(6a)
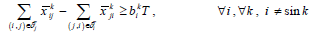 (6b)
(6b)
 (6c)
(6c)
 (6d)
(6d)
In Model 6, T is a free variable the value of whose objective function, T*, determines the network lifetime. Multiplying both sides of constraints 4a-4c by T yields constraints 6b-6d, respectively. One of the drawbacks of Model 6 is that sensors like ECG are more likely to act as routers in this model; therefore they may be forced to receive and transmit the data of other sensors too many times, which leads to a rapid decline in their energy. It is desirable that such sensors should die later as they are of higher importance. In order to overcome this drawback, we first determine a priority for each sensor. Physicians can help, in this regard, to set priorities for sensors and identify important and unimportant sensors as follows: the lower the rank of a sensor is the more important and of higher priority it is. Thus, such a sensor receives a smaller amount of data; that is, the rate of transmitted data toward the sensor is lower. Let’s assume ti is the rank of the ith sensor specified by a physician.
We put 0<ti ≤ 1. Each sensor has a limited capacity, so when tj>ti, the capacities of sensors i and j change to ti ui and tj uj, respectively. Hence, sensor j dies later than sensor i. It is also possible in Model 6 that packets transmitted by sensors may not be completely received by the sink. In this case, it is said that reliable packet transmission is not done properly, and packets may fail to reach the sink due to a variety of reasons. To tackle this problem, we can define a degree of reliability for each sensor. In fact, Ri denotes the reliability of the ith sensor, where i, 0 ≤ Ri ≤ 1. To this end, we define a binary variable Zk such that if sensor i receives the information of sensor k, then Zik=1; otherwise, Zik=0. Let τk be the reliability of the kth sensor’s information reception (0<τk ≤ 1). It is desirable that successful information transfer to the sink should be at least equal to τk.
Thus, the following constraint can be mentioned:
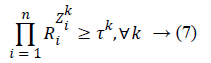
If Zik=1, then RiZik=Ri; that is, sensor i interferes in reliability of the path used for transmitting the data of the kth sensor. In contrast, if Zik=0, then RiZik =1; that is, sensor i does not interfere at all in reliability of the path used for transmitting the data of the kth sensor.
Since Constraints 7 are non-linear, we take the natural logarithm of both sides to make them linear. Therefore,
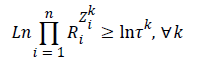
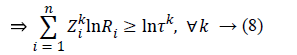
Given that i, Ln Ri=Ṝi and k, Ln τk=τ-k, Constraint 8 changes as follows:
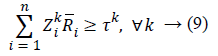
such that
Zki {0, 1} → (10)
Since the information generation rate of a sensor might not be transferable over a given bandwidth, it is desirable to define a capacity for each channel, so with this end in view, we employ Shannon’s equation.
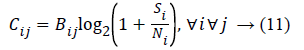
If fact, Cij is the maximum pace at which data can be transferred over the path (i, j) in each second. Bij is the bandwidth of the channel between sensor i and sensor j in Hz, Si denotes the signal related to sensor i in Hz, and Ni represents the amount of noise affecting sensor i. We consider thermal noise in our model. Thermal noise in a bandwidth of Bij Hz can be calculated as follows:
Ni=K.Di.Bij(w/Hz)
Where K represents Kalvin’s constant, and Di denotes the temperature of sensor i.
As discussed previously, the maximum lifetime of a wireless body area sensor network by taking account of the priority of sensors, reliability, and bandwidth can be obtained by the following mixed-integer programming problem:
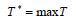
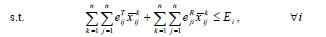 (12a)
(12a)
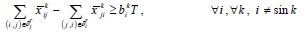 (12b)
(12b)
 (12c)
(12c)
 (12d)
(12d)
 (12e)
(12e)
 (12f)
(12f)
 (12g)
(12g)
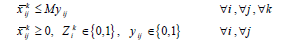 (12h)
(12h)
where M is an extremely large positive number. It is obvious that if Σj=1x̅ji>0, then according to Constraint 12e, Zik=1; that is, sensor i receives the information of sensor k. On the other hand, if , then Zik=0 according to Constraint 12f. Constraint 12g guarantees that all data transmitted from i to j is equal to the maximum capacity of (i, j) in each second. Therefo 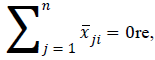 Model 12 provides at least one path for each node, with the energy of sensors, the rank of sensors, reliability, and bandwidth having already been taken into consideration. The network lifetime calculated by Model 6-i.e. without considering reliability, priority, and bandwidth is obviously greater than or equal to that given by Model 12 because adding limitations to Model 6 does not make the feasible region become larger; consequently, the objective function value is not improved, that is, it either remains constant or is worsened, leading to a drop in the network lifetime as maximization problem is concerned. If the imposed limitations don’t make changes to the feasible region of Model 6, then the network lifetime calculated after placing limitations is equal to that measured by Model 6.
Model 12 provides at least one path for each node, with the energy of sensors, the rank of sensors, reliability, and bandwidth having already been taken into consideration. The network lifetime calculated by Model 6-i.e. without considering reliability, priority, and bandwidth is obviously greater than or equal to that given by Model 12 because adding limitations to Model 6 does not make the feasible region become larger; consequently, the objective function value is not improved, that is, it either remains constant or is worsened, leading to a drop in the network lifetime as maximization problem is concerned. If the imposed limitations don’t make changes to the feasible region of Model 6, then the network lifetime calculated after placing limitations is equal to that measured by Model 6.
Evaluating Results and Solving Numerical Examples
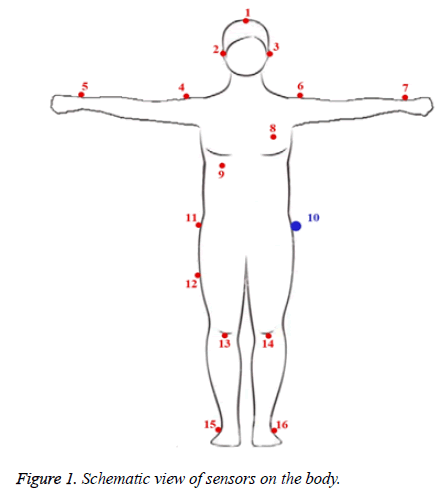
In this section, in order to demonstrate the applicability of the proposed models for the network lifetime maximization, we present a simple example where 15 sensors and one sink are mounted on the body as shown in Figure 1.
We assume that sensor 10 is the sink node, which is solely responsible for gathering data from other sensors and therefore does not function as a biological sensor. Furthermore, since the proposed models are constructed based on patient’s immobility, sensors have been arranged in fixed positions on a particular type of body posture. It is notable that the initial energy of the sink needs to be greater than that of other sensors because it uses bigger batteries to be capable of receiving data from all sensors. The values of energy presented in Table 1 have been selected based on CHipcon cc2420 transceiver, so all sensors have been assumed to have a fixed capacity of 512 KB; however we can use any other parameters for numerical example.
| Sensor | No. | Initial energy | Transmitted energy | Received energy | Transmission rate | Rank/rating | Capacity |
|---|---|---|---|---|---|---|---|
| EEG | 1 | 0.5 J | 96.9 n J/bit | 172.8 n J/bit | 960 b/s | 2 | 512 KB |
| HEARING | 2 | 0.5 J | 96.9n J/bit | 172.8 n J/bit | 100 kbps | 3 | 512 KB |
| HEARING | 3 | 0.5 J | 96.9n J/bit | 172.8 n J/bit | 100 kbps | 4 | 512 KB |
| EMG | 4 | 0.5 J | 96.9n J/bit | 172.8 n J/bit | 8000 b/s | 13 | 512 KB |
| EMG | 5 | 0.5 J | 96.9n J/bit | 172.8 n J/bit | 8000 b/s | 11 | 512 KB |
| EMG | 6 | 0.5 J | 96.9n J/bit | 172.8 n J/bit | 8000 b/s | 14 | 512 KB |
| EMG | 7 | 0.5 J | 96.9n J/bit | 172.8 n J/bit | 8000 b/s | 12 | 512 KB |
| Blood Pressure | 8 | 0.5 J | 96.9n J/bit | 172.8 n J/bit | 800 b/s | 1 | 512 KB |
| ECG | 9 | 0.5 J | 96.9n J/bit | 172.8 n J/bit | 4000 b/s | 5 | 512 KB |
| Sensor (sink) | 10 | 10 J | 96.9n J/bit | 172.8 n J/bit | 250 kbps | 16 | 512 KB |
| Glucose sensor | 11 | 0.5 J | 96.9n J/bit | 172.8 n J/bit | 1600 b/s | 6 | 512 KB |
| Lactic acid | 12 | 0.5 J | 96.9n J/bit | 172.8 n J/bit | 1600 b/s | 15 | 512 KB |
| EMG (Knee) | 13 | 0.5 J | 96.9n J/bit | 172.8 n J/bit | 8000 b/s | 9 | 512 KB |
| EMG (Knee) | 14 | 0.5 J | 96.9n J/bit | 172.8 n J/bit | 8000 b/s | 10 | 512 KB |
| EMG | 15 | 0.5 J | 96.9n J/bit | 172.8 n J/bit | 8000 b/s | 7 | 512 KB |
| EMG | 16 | 0.5 J | 96.9n J/bit | 172.8 n J/bit | 8000 b/s | 8 | 512 KB |
Table 1. Initial values for sensors mounted on the body.
In order to solve the proposed model, it is necessary that values for sensors should thoroughly be specified. The values are given in Table 1.
Since the priority of sensors varies depending on the types of diseases a person suffers from, we have asked a physician to give us the rank of sensors according to the information of a hypothetical patient. Besides, the transmission rate of each sensor has been selected based on the nature of the sensor and the type of data it generates. In Figure 1, there exists a set of neighbors around each sensor toward which the sensor can send its data based on its radio transmission power and the distance between sensors. For example, the neighbors of sensor number 1 are sensors number 3, 2, 4, 5, 6, and 7; that is to say, data transmission toward neighboring sensors is more reasonable, considering radio transmission power and the distance between sensors. We suppose the neighborhood of each sensor in Figure 1 as follow; however can consider any other neighboring set for each sensor.
δT1={(1, 3), (1, 2), (1, 4), (1, 5), (1, 6), (1, 7)}
δT2={(2, 4)}
δT3={(3, 6)}
δT4={(4, 8), (4, 10)}
δT5={(5, 4), (5, 10)}
δT6={(6, 10), (6, 8)}
δT7={(7, 10), (7,6)}
δT8={(8, 10)}
δT9={(9, 10)}
δT11={(11, 10)}
δT12={(12,11), (12, 10)}
δT13={(13, 12), (13, 10)}
δT14={(14, 10)}
δT15={(15, 13), (15, 14), (15, 10)}
δT16={(16, 13), (16, 10), (16, 15), (16, 14)}
The parameters of the reliability of all sensors (Ri), the reliability of receiving the information of sensor k (τk), and the transfer speed of path (i, j) have been assumed to occur randomly. It’s worth mentioning that lnRi and lnτk are used in Model 12; besides, M=107.
Using GAMS software, we run Model 12 so as to calculate the network lifetime according to the mentioned values. Consequently, a path is found for each sensor by considering the energy of sensors, the rank of sensors, reliability, and bandwidth (Table 2).
| Source | Routes to sink |
|---|---|
| 1 | R1: 1-2 -4-10, R2: 1-3-6-10, |
| R3: 1-6-10, R4: 1-7-10 | |
| 6 | R1: 6-8-10 |
| 13 | R1: 13-12-10 |
| 16 | R1: 16-13-12-10, R2: 16-13-10, |
| R3: 16-15-10, R4: 16-14-10 |
Table 2. Paths obtained by solving Model 12 for sensor no. 1, 6, 13 and 16.
As illustrated in Table 2, sensor no. 1 uses different pathsdepicted by distinct colors-to transmit its own data toward the sink, which is represented by number 10. While sensors no. 4, 5, 7, 8, 9, 11, 12, 14, and 15 employ direct data transmission, sensors no. 1, 6, 13, and 16 take advantage of different paths for transmitting their data to the sink.
According to what was previously mentioned and after solving Model 12, the objective function value-being the lifetime of the wireless body area network under evaluation is obtained as T*=62.866 time units.
Next, we consider different forms of the proposed model and compare them with star and double-hop methods to demonstrate the applicability of the model. In the Star method, all sensors communicate with the sink directly. In the doublehop method, however, all sensors transmit their data to predetermined intermediate nodes which subsequently forward the data toward the sink.
According to the properties of linear programming problems, it is obvious that the feasible region does not become smaller by removing limitations, so the objective function value will not decline, i.e. it either increases or remains unchanged. Hence, when Constraint 12C is changed as , Model 12 calculates the network lifetime without considering priority. In this case, the value of the objective function remains unchanged, that is, th 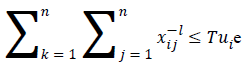 network lifetime after removing priorities is 62.866 time units.
network lifetime after removing priorities is 62.866 time units.
As we know, each sensor transmits its own data directly to the sink in the Star method, which despite simplicity, results in increased energy consumption. Since direct data transmission demands higher transmission power, the energy of sensors is exhausted too early, leading to a fall in the network lifetime. According to the studied parameters, the network lifetime given by the Star method is quite insignificant (10-1 time units) compared to that calculated by Model 12.
Next, we assume that data is transmitted toward the sink in a multi-hop mode, with sensors no. 9 and 12 serving as intermediate nodes. That is to say, Δ1=9 and Δ2=12 play the role of intermediate nodes, receiving data from other sensors and then sending it to the sink. Therefore, all sensors transmit their data to sensor 9 or sensor 12 based on their distance from these two sensors; the received data by sensors 9 and 12 is then forwarded to the sink.
Sensors ΓΔ1={1, 2, 3, 4, 5, 6, 7, 8, 11} send their data to the sink through Δ1; likewise, sensors ΓΔ2={13, 14, 15, 16} transmit their data to the sink through Δ2. Thus, the network lifetime when data is transmitted in a double-hop mode is calculated as follows:
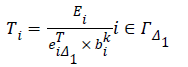
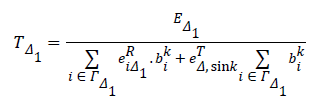
Similarly, ΓΔ2 can be calculated. Hence, the network lifetime is given by:
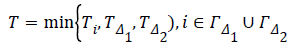
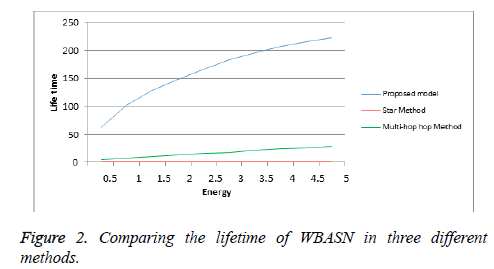
According to the parameters used in Model 12, the network lifetime in this case is 4.968 time units. The reason for the short network lifetime in the double-hop method is excessive use of sensors Δ1 and Δ2, which exhausts the energy of sensors and ultimately kills them off. Obviously, the lifetime of the entire network decreases as well. Overall, the results can be summarized in Table 3.
| Multi-hop method | Star method | The proposed model |
|---|---|---|
| 4.968 | 10-1 | 62.866 |
Table 3. The network lifetime.
It should be noted that the results presented in Table 3 change as the initial input parameters are changed.
Furthermore, given the increase in the initial energy of sensors, the network lifetime increases in all three of the abovementioned methods (Figure 2). Moreover, the network lifetime is more appropriate in the proposed model than the other two methods.
Conclusions
Given the increasing use of wireless body area sensor networks as a way of caring for patients, it is substantially important to prolong the lifetime of these networks because to set up and mount these sensors on a patient’s body is no easy task and requires spending a great deal of time and money. Safe transmission of vital signs data toward the sink and finally to a given medical center is of immense importance; furthermore, the significance of different sensors varies from person to person depending on the physician’s opinion and the types of diseases a patient suffers from. Hence, we have proposed a model in this paper to maximize the network lifetime while taking account of limitations such as rank of sensors, reliability of sensors, and bandwidth. In addition to solving the presented model in different cases, we have compared our model with star and double-hop transmission methods. Results show that the proposed model-due to the balanced use of all sensors in compliance with the limitations of temperature, reliability, rank, and bandwidth-brings a significant improvement in the network lifetime. Moreover, the survival time of important sensors is more reasonable with the proposed model as compared to the other methods. It should be noted that the network lifetime increases or remains the same after each of the limitations is removed. In the future, a robust model corresponding to the proposed one can be achieved by considering uncertainty for each of the parameters.
References
- Gupta SK, Mukherjee T, Venkatasubramanian KK. Body area networks: safety, security, and sustainability. Cambridge Univ Press 2013.
- Zhao N, Ren A, Zhang Z, Zhu T, Rehman MU, Yang X, Hu F. Patterns-of-life aided authentication. Sensors 2016; 16: 1574.
- Wang J, Wang Q. Body area communications: channel modeling, communication systems, and EMC. John Wiley Sons 2012.
- Deepak K, Babu AV. Improving energy efficiency of incremental relay based cooperative communications in wireless body area networks. Int J Commun Syst 2015; 28: 91-111.
- Hu H, Yang Z. Cooperative opportunistic routing protocol for wireless sensor networks. Wireless Commun Netw Mob Comp Int Conf 2007; 2551-2554.
- Argyriou A, Breva AC, Aoun M. Optimizing data forwarding from body area networks in the presence of body shadowing with dual wireless technology nodes. IEEE Trans Mob Comput 2015; 14: 632-645.
- Effatparvar M, Dehghan M, Rahmani M. A comprehensive survey of energy-aware routing protocols in wireless body area sensor networks. J Med Sys 2016; 40: 201-228.
- Abbasi UF, Awang A, Hamid NH. A cross-layer opportunistic MAC/routing protocol to improve reliability in WBAN. Commun Asia-Pacific Conference 2014; 36-41.
- Ahmed S, Javaid N, Akbar M, Iqbal A, Khan ZA, Qasim U. LAEEBA: Link aware and energy efficient scheme for body area networks. In Advanced Information Networking and Applications (AINA). IEEE 28th Int Conf 2014; 435-440.
- Cai X, Li J, Yuan J, Zhu W, Wu Q. Energy-aware adaptive topology adjustment in wireless body area networks. Telecommun Sys 2015; 58: 139-152.
- Liao Y, Leeson MS, Higgins MD. Flexible quality of service model for wireless body area sensor networks. IET Healthc Technol Lett 2016; 3: 12-15.
- Elias J. Optimal design of energy-efficient and cost-effective wireless body area networks. Ad Hoc Networks 2014; 13: 560-574.
- George S, Nikos D, Rosario S, Valeria L, Fortino G, Yiannis A. Decentralized time-synchronized channel swapping for Ad hoc wireless networks. IEEE Trans Veh Technol 2016; 10: 8538-8553.
- Razzaque MA, Javadi SS, Coulibaly Y, Hira MT. QoS-aware error recovery in wireless body sensor networks using adaptive network coding. Sensors 2014; 15: 440-464.
- Liang XL, Shen X, Lu Q, Lin R, Shen X, Zhuang XW. Exploiting prediction to enable secure and reliable routing in wireless body area networks. Proc IEEE INFOCOM Orlando Florida USA 2012; (pp. 388–396).
- Ahmad, A, Javaid, N, Khan, Z. A, Imran, M, Alnuem, M. iA-MAC: Improved adaptive medium access control protocol for wireless body area networks. In Communications and Information Technologies (ISCIT) 2014, 14th International Symposium on (pp. 156-160), IEEE.
- Bag A, Bassiouni M. Energy efficient thermal aware routing algorithms for embedded biomedical sensor networks. Mob Adhoc Sensor Sys IEEE International Conference 2006; 604-609.
- Takahashi D, Xiao Y, Hu F. LTRT: Least total-route temperature routing for embedded biomedical sensor networks. IEEE GLOBECOM IEEE Glob Telecommun Conf 2007.
- Tang Q, Tummala N, Gupta SK, Schwiebert L. TARA: thermal-aware routing algorithm for implanted sensor networks. Distr Comp Sensor Sys 2005; 206-217. Javaid N, Ahmad A, Nadeem Q, Imran M, Haider N. iM-SIMPLE: iMproved stable increased-throughput multi-hop link efficient routing protocol for wireless body area networ. Comp Human Behav 2014.
- Nikoletseas S, Raptis TP, Souroulagkas A, Tsolovos D. Wireless power transfer protocols in sensor networks: experiments and simulations. J Sens Actuator Netw 2017; 6: 4.
- Chen X, Xu Y, Liu A. Cross layer design for optimizing transmission reliability, energy efficiency, and lifetime in body sensor networks. Sensors (Basel) (Switzerland) 2017; 17.
- Rostampour A, Moghim N, Kaedi M. A new energy-efficient topology for wireless body area networks. J Med Signals Sens (India) 2017; 7: 163-169.
- Yu J, Park L, Park J. CoR-MAC: contention over reservation MAC protocol for time-critical services in wireless body area sensor networks. Sensors (Basel) (Switzerland) 2016; 16.
- Zhang Y, Zhang B, Zhang S. A lifetime maximization relay selection scheme in wireless body area networks. Sensors 2017; 17: 1267.
- Latre B, Braem B, Moerman I, Blondia C, Demeester P. A survey on wireless body area networks. Wireless Netw 2011; 17: 1-18.