ISSN: 0970-938X (Print) | 0976-1683 (Electronic)
Biomedical Research
An International Journal of Medical Sciences
- Biomedical Research (2016) Volume 27, Issue 2
Preliminary investigations on automatic segmentation methods for detection and volume calculation of brain tumor from MR images.
| Swathi K1 and Kishore Balasubramanian2* 1Applied Electronics, Dr. Mahalingam College of Engineering and Technology, India 2Department of EEE, Dr. Mahalingam College of Engineering and Technology, India |
| Corresponding Author: Kishore Balasubramanian, Department of EEE, Dr.Mahalingam College of Engineering and Technology, India |
| Accepted: February 16, 2016 |
Combining image segmentation based on the statistical classification with geometric prior information is supposed to increase robustness and reproducibility. A probability density function is initialized and a spatial constraint is defined which prevent segmentation that is not a part of the model. The goal of this work is a high quality image segmentation of healthy tissue and a precise delineation of tumor boundaries from multiple slices of MRI data. In this paper, algorithms like K-means, Watershed and Expectation Maximization algorithms are used for the investigation and the results of all the segmentations are compared. Based on the results, a common consensus on the robustness of each method is discussed. The Watershed segmentation and the Atlas are combined through markers and this has been applied in the Gray/White matter segmentation in MR images. A previous probability criterion is to be used for its calculation. These methods act as an aid in the early detection of many neurological disorders like Brain tumor, Paralysis, Alzheimer’s disease, etc. They also handle types of pathology, space occupying mass tumors, and infiltrating changes like edema aiding as a new technique for clinical routine for use in planning and monitoring in neurosurgery, radiology and radio-oncology. These methods can be enhanced to delineate tumor from surrounding tissues like edema aiding in image guided surgery. Both the off-line data and live patient data are used for the analysis. Testing of different algorithms for their robustness in segmenting the brain images are carried out using the image processing tool (IPT) of MATLAB.
Keywords |
||||||||||
| Image segmentation, Brain tumor MRI, Segmentation, Tissue classification, Morphological operations, Probabilistic brain atlas. | ||||||||||
Introduction |
||||||||||
| Medical Image Segmentation has become an important diagnostic tool in the practice of modern medicine. Segmentation of MRI Brain images is the delineation of neuroanatomical structures as well as brain abnormalities. The study of many brain disorders involves the accurate segmentation of Magnetic Resonance (MR) images of the brain. Such studies typically involve large amount of data and manual tracing by a human expert which is time-consuming. In addition, human experts show significant intra- and inter-observer variability, which complicates the analysis of the resulting image segmentations. Hence, there is a need for automated methods that produce fast, reliable and reproducible segmentations. | ||||||||||
| There are mainly three main goals on segmentation of human brain images: | ||||||||||
| • Brain volume extraction | ||||||||||
| • Brain tissue segmentation | ||||||||||
| • Specific brain structure delineation | ||||||||||
Problem definition |
||||||||||
| The problem addressed here is the automatic post-acquisition segmentation of brain tumors and associated edema in multi spectral Magnetic Resonance (MR) images. The input is a series of slices taken from different MR modalities and the output will be a binary segmentation of the images, where each pixel in the input image is labeled as either normal or abnormal. This work specifically addresses the more challenging tasks of segmenting namely the Gross Tumor Volume (GTV) and the Full Tumor Area (FTA). The desired output is defined manually by human experts based on the visible abnormality in the image data, which is limited by the imaging protocol, used and is subjected to interpretation. In order for the algorithm to be practically useful for segmenting existing data, two major constraints are required. The first major constraint is that the processing will be a post acquisition. Specifically, only the image data will be used in order to produce the final result. The second major constraint is that the system must be able to utilize common MR modalities (such as T1-weighted and T2-weighted images). | ||||||||||
Magnetic resonance imaging and brain tumors |
||||||||||
| Magnetic Resonance Imaging (MRI) is a powerful visualization technique that allows images of internal anatomy to be acquired in a safe and non-invasive way. It is based on the principles of Nuclear Magnetic Resonance (NMR), and allows a vast array of different types of visualizations to be performed. This imaging medium has been of particular relevance for producing images of the brain, due to the ability of MRI to record signals that can distinguish between different ‘soft’ tissues (such as gray matter and white matter). In imaging the brain, two of the most commonly used MRI visualizations are T1-weighted and T2-weighted images. These weightings refer to the dominant signal (whether it be the T1 time or the T2 time) measured to produce the contrast observed in the image. In visualizing brain tumors, a second T1- weighted image is often acquired after the injection of a ‘contrast agent’. These ‘contrast agent’ compounds usually contain an element whose composition causes a decrease in the T1 time of nearby tissue (gadolinium is one example). This result in bright regions observed at image locations that contain ‘leaky’ blood cells (where blood moves through the brainblood barrier). The presence of this type of ‘enhancing’ area can indicate the presence of a tumor. | ||||||||||
Goal |
||||||||||
| The goals of this work are organized as | ||||||||||
| • To compare the performance analysis of segmentation techniques for the MR images of the human brain such as Expectation Maximization (EM), k-means clustering, and Watersheds. There is no single algorithm that can be universally used to solve all problems. So the goal is to search for the best algorithms that can be used to segment medical images. | ||||||||||
| • To validate all these segmentation algorithms with live patient data and check for the robustness of the algorithms based on the exact quantum of tumor present in the subject information and the time complexity involved to carry out the segmentation task. | ||||||||||
Assumptions |
||||||||||
| As one would expect, making certain assumptions and using prior knowledge can help greatly in the problem of segmenting brain tumors. It is assumed that tumors are ring-enhancing or fully enhancing with contrast agent. Intravenous MRI contrast agents, specifically the gadolinium chelates having high safety and lack of nephrotoxicity compared with X-ray contrast media is used in obtaining the MR images. The major tumor classes that fall in this category are meningiomas and malignant gliomas. | ||||||||||
MR sequences |
||||||||||
| It is assumed that all datasets analyzed include a T1 precontrast image, a T1 post-contrast image (both with 1 × 1 × 1.5 mm3 voxel dimensions), and a T2 image (1 × 1 × 3 mm3 voxel dimensions). This inter-slice spacing is the standard protocol at the hospitals where the datasets were acquired. All the datasets are acquired on Siemens 1.5T and 3T scanners. The Siemens MRI enables to detect different pathology very early, as it may be seen with CT scan. It also allows characterizing the type of abnormality seen and visualizing the extent of problem better. | ||||||||||
Segmentation Methods |
||||||||||
| Several automated technique have been developed for MRI segmentation. Several automated segmentation techniques and their performance are discussed below. | ||||||||||
Thresholding |
||||||||||
| One of the simplest and oldest image segmentation techniques is the thresholding process. It consists of separating pixels in different classes depending on their gray levels. An intensity value, called the threshold that separates the desired classes is determined. Based on the threshold value, pixels are grouped with intensity greater than the threshold into one class and remain pixels grouping into another class. The demerit is that it cannot be applied to multichannel images. In thresholding technique, the image has only two values either black or white. MR image contains 0 to 255 grey values. Hence, thresholding of MR images ignores the tumor cells [1]. Hence this technique is not considered for analysis. | ||||||||||
Clustering techniques |
||||||||||
| Clustering means collection of objects which are similar between them and are dissimilar objects belonging to other clusters. Clustering is suitable in biomedical image segmentation when the number of cluster is known for particular clustering of human anatomy. There are two types of Clustering algorithm i) Exclusive clustering ii) Overlapping clustering | ||||||||||
| In exclusive clustering, one data (pixel) is belonging only one cluster then it could not belong to another cluster. K-mean is example of exclusive clustering algorithm. In overlapping clustering, one data (pixel) is belonging two or more clusters. Fuzzy C means is example of overlapping clustering algorithm [2]. | ||||||||||
K-means clustering |
||||||||||
| The k-means algorithm is an algorithm to cluster objects based on attributes into ‘k’ partitions. It assumes that the object attributes form a vector space. The objective is to minimize the total intra-cluster variance, or the squared error function, where there are k clusters, Si, i=1, 2...k and μi is the centroid or mean point of all the points. | ||||||||||
| The algorithm starts by partitioning the input points into ‘k’ initial sets, either at random or using some heuristic data. It then calculates the mean point, or centroid, of each set. It constructs a new partition by associating each point with the closest centroid. Then the centroids are recalculated for the new clusters, and algorithm repeated by alternate application of these two steps until convergence, which is obtained when the points no longer switch clusters (or alternatively centroids are no longer changed). | ||||||||||
| The algorithm has remained extremely popular because it converges extremely quickly, in practice. In fact, many have observed that the number of iterations is typically much less than the number of points. Approximate k-means algorithms have been designed that make use of core sets: small subsets of the original data [1,3]. | ||||||||||
Algorithm |
||||||||||
| Step 1: Choose first K different feature vectors as K different cluster centers c0(0), c1(0)… c k-1(0), where K is the number of classes and the superscript denotes the iteration number. | ||||||||||
| Step 2: At r-th iteration for each of the feature vectors, assign feature vector {fi} to cluster Ck if | ||||||||||
| for j=0, 1,…, K-1 where d is a distance measure, or Euclidean distance. | ||||||||||
| Step 3: New cluster centers are computed by minimizing intraclass distances. If ck(r) is the center of ck at r-th iteration, this is calculated by minimizing | ||||||||||
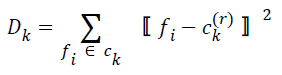 |
||||||||||
| for k=0, 1, 2, … , K-1. The cluster center obtained by minimizing Dk in the above equation is the mean value of feature vectors belonging to Ck at r-th iteration, i.e.s | ||||||||||
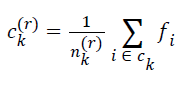 |
||||||||||
| where nk(r) is the number of feature vectors assigned to ck at rth iteration | ||||||||||
| Step 4: If ck(r)=ck(r-1) for all k, that means there are insignificant or no changes in cluster centers, then the algorithm is terminated, else continue from Step 2. | ||||||||||
Summary |
||||||||||
| K-means has invited a lot of attention for its simplicity and speed which allows it to run on large datasets. In terms of performance, the algorithm is not guaranteed to return a global optimum. The quality of the final solution depends largely on the initial set of clusters, and may, in practice, be much poorer than the global optimum. Since the algorithm is extremely fast, a common method is to run the algorithm several times and return the best clustering found. | ||||||||||
| Another main drawback of the algorithm is that the number of clusters (i.e. ‘k’) to find is to be specified in advance. If the data is not naturally clustered, some strange results may be expected. Also, the algorithm works well only when spherical clusters are naturally available in data. Thus, the K-means algorithm has the following disadvantages: (1) supervised learning mode, (2) slow real-time ability, (3) instability. | ||||||||||
Watershed |
||||||||||
| The concepts of watersheds and catchment basins for image segmentation are borrowed from topography in which watershed lines divide individual catchment basins. Image data can be interpreted as a topographic surface with the gray levels of its gradient image representing the altitudes. Homogeneous regions correspond to catchment basins and region boundaries correspond to high watersheds. The image segmentation problem is hence reduced to find the watershed lines or equivalently the catchment basins. There are two basic approaches to watershed image segmentation: the top-down approach and the bottom-up approach. Both start with identifying local minima in the gradient image. A local minimum is a connected region of pixels (could be only one) with the same gray levels whose neighbors have higher altitudes. In the top-down approach, each pixel of the image is taken as a water drop and flow downstream to a local minimum. A catchment basin is then defined as the set of pixels that flow to the same local minimum [4]. | ||||||||||
| While the downstream flow path is intuitive and easy to determine in the continuous space, there exists no rule to set up the path uniquely in digital surfaces. The bottom-up approach is more suitable to practical implementation. Raw watershed segmentation produces a severely over-segmented image with much more catchment basins than expected. To overcome the problem, various region-merging methods can be used. One simple method of basin merging method is to use a water depth threshold. The threshold is the maximum depth that the topographical surface is immersed into the water. Then any catchment basin that is completely immersed in the water is merged with its adjacent basins [5]. | ||||||||||
Algorithm |
||||||||||
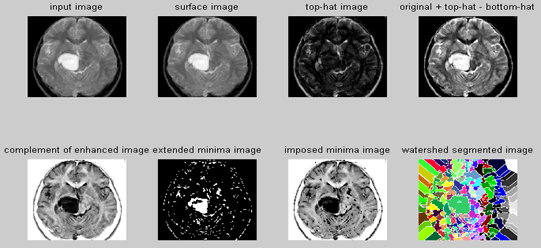
| Step 1: Read Image-Read in the 'afmsurf.tif' image, which an atomic force microscope image of a surface is coating. | ||||||||||
| Step 2: Maximize Contrast | ||||||||||
| To minimize the number of valleys found by the watershed transform, maximizing the contrast of objects of interest is needed. A common technique for contrast enhancement is the combined use of the top-hat and bottom-hat transforms. | ||||||||||
| Step 3: Subtract Images | ||||||||||
| It is seen that the top-hat image contains the "peaks" of objects that fit the structuring element. In contrast, the bottom-hat image shows the gaps between the objects of interest. To maximize the contrast between the objects and the gaps that separate them from each other, the "bottom-hat" image is subtracted from the "original + top-hat" image. | ||||||||||
| Step 4: Convert Objects of Interest | ||||||||||
| Recall that watershed transform detects intensity "valleys" in an image. The imcomplement function is used on our enhanced image to convert the objects of interest to intensity valleys. | ||||||||||
| Step 5: Detect Intensity Valleys | ||||||||||
| All intensity valleys below a particular threshold are detected with the imextendedmin function. The output of the imextendedmin function is a binary image. The location rather than the size of the regions in the imextendedmin image is important. The imimposemin function will modify the image to contain only those valleys found by the imextendedmin function. The imimposemin function will also change a valley's pixel values to zero (deepest possible valley for uint8 images). All regions containing imposed minima will be detected by the watershed transform. | ||||||||||
| Step 6: Watershed Segmentation | ||||||||||
| Watershed segmentation of the imposed minima image is accomplished with the watershed function. | ||||||||||
| Step 7: Extract Features from Label Matrix | ||||||||||
| Features can be extracted from the label matrix with the regionprops function. For example, two measurements (area and orientation) are calculated and viewed as a function of one another. | ||||||||||
Summary |
||||||||||
| Marker selection can range from simple procedures as used above to very complex methods involving size, shape, location, relative distances, and texture content and so on. The usage of internal and external markers brings a priori knowledge to bear on the segmentation problem. Humans often aid segmentation and higher level tasks in everyday vision by using a priori knowledge. Thus, the fact that segmentation by watersheds offers a framework that can make effective use of this type of knowledge is a significant advantage of this method. | ||||||||||
| However, watersheds have a major drawback in forming the catchment basins exactly to the shape of the given image. Hence, they are the better algorithm for segmentation of art images but not frequently used for segmentation of medical images. | ||||||||||
Expectation Maximization |
||||||||||
| For the task of segmenting head MR images into the three normal brain classes (grey matter, white matter, and cerebrospinal fluid), Expectation Maximization have shown to be robust to both intensity in-homogeneity and intensity non standardization. This algorithm consists of an Expectation step where the tissue class parameters are computed given the current estimation of the in-homogeneity field, and a Maximization step where the in-homogeneity field is computed given the current estimation of the tissue class parameters. This algorithm interleaves Probability Density Function (PDF) estimation for each tissue class (gray matter, white matter, and CSF), classification, and bias field correction using the classic EM approach. The EM Segmentation algorithm (EMS) uses a spatial atlas from the Statistical Parametric Mapping (SPM) package for initialization and classification. The SPM atlas contains spatial probability information for brain tissues. It was created by averaging segmentations of normal subjects that had been registered by an affine transformation. This spatial atlas is registered to the patient data, with an affine transformation, providing spatial prior probabilities for the tissue classes. The PDFs are then initialized based on the atlas probabilities. The algorithm depends on T1 pre- and post-contrast images from MRI. | ||||||||||
Algorithm |
||||||||||
| Identify the intensity and spatial outliers and detect the abnormalities. | ||||||||||
| 1. Initial densities for normal brain tissues obtained using probabilistic brain atlas. | ||||||||||
| 2. Image data is registered via affine transformation. | ||||||||||
| 3. Training samples is constrained to be voxels (p=85%). | ||||||||||
| 4. MCD technique is used in location and dispersion of samples. | ||||||||||
| 5. Trimming training samples done by MST and edge breaking. | ||||||||||
| 6. Estimate PDF for each class and locate the voxels with abnormal intensities (regions with low posterior probabilities) | ||||||||||
| 7. Then the density approximation is done using Kernel expansion, where the bandwidth set is to be 4% of the data range and Class the label including gray & white matter, CSF, etc. | ||||||||||
Summary |
||||||||||
| A model-based segmentation method is developed for segmenting head MR image datasets with tumors and infiltrating edema. This is achieved by extending the spatial prior of a statistical normal human brain atlas with individual information derived from the patient's dataset. Thus, the statistical geometric prior with image-specific information for both geometries of newly appearing objects is combined, and probability density functions for healthy tissue and pathology. This procedure can handle large variation of tumor size, interior texture, and locality. The method provides a good quality of healthy tissue structures and of the pathology, a requirement for surgical planning or image-guided surgery. This allows the algorithm to be fully automatic. | ||||||||||
Results |
||||||||||
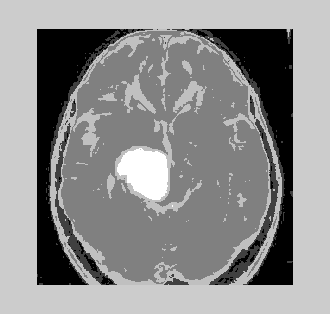
| The result of the algorithms used has been shown in the following figures 1-3A and 3B simulated using MATLAB with an input obtained from a scan center (25 sets of real data) and offline images [6-8]. MR pulse spin echo sequence parameters used in the analysis are: | ||||||||||
| 1. Gadolinium enhanced, fat suppressed T1 weighted image with TE < 30, TR < 800, flip angle 90° | ||||||||||
| 2. Fat suppressed, fluid attenuated T2 weighted image with TE > 80, TR > 2000, flip angle 90° | ||||||||||
Conclusion |
||||||||||
Performance analysis |
||||||||||
| Performance analysis of segmentation algorithms, viz. K-means, Watersheds and Expectation Maximization algorithms has been compared both quantitatively and qualitatively for simulated MR brain images. In order to compare the performances quantitatively, the same definition of an error measure can be adopted in terms of the misclassification rate, which is defined as the number of pixels misclassified by the algorithm divided by the total number of pixels in the image. | ||||||||||
| The table 1 summarizes the error measures obtained by the three methods when applied on a T-1 weighted [1-mm thickness, 3% noise, 20% INU, X=0.0, Y=-18.0, Z=14.0] simulated MR images. From the table, we find that the performance of the average MCR is same for EM and Watersheds and is slightly less for K-means. | ||||||||||
| The results presented in the above table 2 show that the performance of the proposed methods, while segmenting the T-2 weighted [1-mm thickness, 0% noise, 0% INU, X=0.0, Y=-18.0, Z=24.0] simulated MR brain images. The results presented in the above table show that the performance of K-means and EM is better than Watershed. | ||||||||||
| The performance of these algorithms can also be validated based on two important parameters: | ||||||||||
| 1. Time Complexity of the algorithm used | ||||||||||
| 2. Volume of Tumor occupancy shown by different algorithms | ||||||||||
| It is very essential to find the volume of the tumor for better accurate results. The area is determined by selecting the tumor region and calculating the pixel values and adding the values. This method will provide a good result with less effort. The algorithms are validated taking into account certain considerations. The output obtained by using different algorithms is derived from same input image. It is inferred that by initializing the number of clusters equal to 10 for K-means and that of EM is 5, the results obtained are identical. As the number of clusters increases, the results obtained from K-means algorithm will be better. The following were tested with a database of 100 MRI brain images (both online and offline). The inference is analyzed for two broad categories (Table 3). | ||||||||||
| • Non-Tumorous image (Normal Brain) | ||||||||||
| • Abnormal Tissue | ||||||||||
| Non-Tumorous (Normal Brain): The time complexity involved is measured in seconds and the volume occupied by the tumor is measured in percentage volume of the tumor occupied with respect to total volume of the image. For a tumorous image analyzed, the following results are obtained (Table 4). | ||||||||||
| Tumorous Tissue (Abnormal Brain): The time complexity involved is measured in seconds and the volume occupied by the tumor is measured in percentage volume of the tumor occupied with respect to total volume of the image. | ||||||||||
Statistical set |
||||||||||
| Any quantitative decisions about a process or a scheme can be made effective by a mechanism of providing a statistical test. The aim is to determine whether there is enough evidence to "reject" a speculation or hypothesis about the process made. Axial view images of brain MRI are tested using a confusion matrix, which normally consist of information about actual and predicted classifications which is done by a classification system. A confusion matrix illustrates the number of correct and incorrect predictions made by the model compared with the actual classifications in the test data. Performance of such systems is normally calculated by using the data in the matrix. A total of 25 axial view images were handled to test the effectiveness of the algorithms [through images obtained from scan center and literature. Sensitivity and specificity are the two statistical measures of the performance of a binary classification test in addition to accuracy. In statistics it is also known as classification function. Sensitivity measures the percentage of actual positives values which are correctly identified whereas specificity measures the percentage of negative values which are correctly identified. The classification was based on the confusion matrix which consists of True Positive (TP), True Negative (TN), False Positive (FP), and False Negative (FN). The images which are collected from the database were normal as well as cancerous brain images. In this paper there are total 25 test cases in which 14 cases are TP. Sometimes, test results show cases of no tumor but there will be actual tumor present. These are called FN. There are 8 such cases in our test. Some cases don't have the tumor, and the test says they don't, they are TN and in our test there are 2 such cases. Finally the set showed a normal brain MRI image and have a positive test result, called as FP; only one case was recorded in the set. FNs and FPs are significant issues in medical testing. The following table 5 illustrates the results obtained in terms of Accuracy, Sensitivity and Specificity when tested on the data using the above mentioned algorithms. | ||||||||||
Observation |
||||||||||
| It is observed from the findings that Watershed algorithm segments the image in a lesser time than the other algorithms, but as mentioned before, the algorithm faces the problem of forming the catchment basins for complicated images. With normal tissue the Watershed Algorithm shows reduced time complexity. The K-means algorithm takes some time to segment the image as the cluster size is increased in order to obtain good results. | ||||||||||
| It is also observed that the volume of tumor analyzed by different algorithms show almost equal percentage of tumor. The EM algorithm shows fairly good results in terms of time required to execute the segmentation process as well as the volume of delineation present. The patient data was derived from an MRI center and duly attested by a medical expert. The above data was used for the analysis and it has been shown that results closely match with that of the medical expert’s interpretation thereby, the robustness of the algorithms has been proved effective. The datasets collected in which tumor is present mainly had meningioma as the other tumor glioma, was very rare to be found with its ragged boundaries. | ||||||||||
| This tumor segmentation framework has been applied to different datasets, including a wide range of tumor types and sizes. The All datasets were registered to the atlas using information registration. A model-based segmentation method for segmenting head MR image datasets with tumors has been developed. This is achieved by extending the spatial prior of a statistical normal human brain atlas with individual information derived from the patient's dataset. Applications to different tumor patients with variable tumor appearance demonstrated that the procedure can handle large variation of tumor size, interior texture, and locality. | ||||||||||
Future scope |
||||||||||
| The automated segmentation techniques provide a wide range of applications like image guided surgery, volume visualization of regions of interest, medical diagnosis and serves an aid to detect other neurological diseases. Though automated, it requires verification of results from a doctor (to be certified by a competent medical professional before starting treatment). It is also seen from the table that accuracy obtained by individual methods on an average is not convincing. Hybrid algorithms may reduce time complexity further, give accurate area of tumor occupied and aim in improving the accuracy, sensitivity and specificity [9,10]. | ||||||||||
Tables at a glance |
||||||||||
|
||||||||||
Figures at a glance |
||||||||||
|
||||||||||
References |
||||||||||
|